Un problème avec une borne sup

par **Coast** » 28 Sep 2009, 19:45

Bonsoir

Je fais appel à vous concernant un point que je n'arrive pas à résoudre. Merci de m'aider si possible. Toute remarque, aide est al bienvenue. L'exercice est le suivant:

On note

et on définit sur E la relation:

On nous demande de représenter graphiquement l'ensemble des majorants, ça j'y arrive aucun soucis. On nous pose après la question suivante:

Soit A une partie non vide de E. Montrer que A admet une borne supérieure.

Merci de votre aide.

par **zenaf** » 28 Sep 2009, 20:09

Bonjour!
Fait un tour sur http://fr.wikipedia.org/wiki/Lemme_de_Zorn

par **Coast** » 28 Sep 2009, 20:15

zenaf a écrit:Bonjour!
Fait un tour sur http://fr.wikipedia.org/wiki/Lemme_de_Zorn

Bonsoir Zena

Merci je vais regarder ça et je te dirais si j'y arrive.

par **Coast** » 28 Sep 2009, 20:22

zenaf a écrit:Bonjour!
Fait un tour sur http://fr.wikipedia.org/wiki/Lemme_de_Zorn

deux choses:

1) je n'y comprend presque rien !!

2) on n'a pas vu le Lemme de Zorn au cours. Il doit y avoir une façon plus simple de procéder ...

par **Doraki** » 28 Sep 2009, 20:50

En effet on a pas besoin du lemme de Zorn, on peut construire la borne sup d'une partie de E sans passer par l'axiome du choix.

Comment tu trouves le maximum d'une partie finie de E ?

par **Coast** » 28 Sep 2009, 22:00

Angélique_64 a écrit:1) Juste pour vérifier, tu as trouvé quoi comme ensemble des majorants?

2) Sinon tu peux construire une borne supérieure en regardant le sup des premières coordonnées des éléments de A et en bricolant selon les 2 cas qui peuvent se présenter.

le bricolage devrait donner (1,1) !!! mais je me dis qu'une partie de E peut avoir comme borne sup (1/2, tout ce qu'on veut) ou tout autre chose ...

pour ce qui est des majorants,en fait c'est l'intrsection des

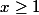
et

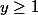
, c'est ce que j'ai trouvé et ça m'a l'air bon.

par **Coast** » 28 Sep 2009, 22:03

Doraki a écrit:En effet on a pas besoin du lemme de Zorn, on peut construire la borne sup d'une partie de E sans passer par l'axiome du choix.

Comment tu trouves le maximum d'une partie finie de E ?

Bah disons une partie finie peut être un ouvert et dans ce cas si on avait un signe strict inférieur des deux cotés j'aurais tendance à penser qu'il y aura pas de borne sup.

mais enfin une borne sup c'est par définition le plus petit des majorants

par **arttle** » 28 Sep 2009, 22:05

Je me servirais du théorème de l'existence de la borne supérieure d'une partie bornée de R deux fois. Une fois pour les x et une fois pour les y. Tu obtiendra normalement la borne supérieure de ton A.

par **Coast** » 28 Sep 2009, 22:15

arttle a écrit:Je me servirais du théorème de l'existence de la borne supérieure d'une partie bornée de R deux fois. Une fois pour les x et une fois pour les y. Tu obtiendra normalement la borne supérieure de ton A.

j'y ai pensé aussi. Le Théorème dit que si A est majorée alors A admet une borne sup. Mais je n'arrive pas à mettre ça sous forme d'une démonstration rigoureuse.

par **arttle** » 28 Sep 2009, 22:21

En fait ta borne supérieure à quoi va-t-elle ressemblée?
En x ça sera la borne supérieure de la première coordonnée de tous les éléments de A
Ensuite pour le y soit le x n'est pas atteint alors la borne supérieure est (x,-1)
soit le x est atteint, et le y est la borne supérieure de {t, (x,t)\in A}

par **Coast** » 03 Oct 2009, 15:57

Bonjour tout le monde

je n'ai pas compris ta démonstration Artt

ma question est toujours d'actualité et je n'arrive toujours pas à résoudre la question. Un idée si possible ?

en vous remerciant d'avance

Un problème avec une borne sup

Un problème avec une borne sup

Qui est en ligne