Partie entière et système d'équation :)

[Anael76]

Bonjour je vous propose un petit exercice :happy2: :
On considère le système suivant

x|x|+y|y|=1
E(x)+E(y)=1
d'inconnue (x,y) € R² .

1/Résoudre graphiquement ce système en représentant d'abord,dans le plan rapporté à un repère orthonormé,
A={ M(x,y) / x|x|+y|y|=1 }
et B={ M(x,y) / E(x)+E(y)=1 }

Personnellement je comprends même pas l'énoncé..... :triste: et je suis totalement perdu, si quelqu'un aurait la gentillesse de m'aider je lui en serais vraiment très reconnaissante ! :ptdr: A noté que l'exercice est tiré de l'olympiade de mathématique d'Espagne 1993 :marteau:

[gandalfcorp]

Réponse rapide sans garantie

E(x)+E(y)=1 alors forcement soit (x,y)=(0,1) soit (x,y)=(1,0)

Du coup je vois pas l'intérêt de la deuxième équation puisque ces deux couples la vérifie

Mais bon, pour la représentation graphique, je traiterai 4 cas, un pour chaque cadran du plan afin de faire sauter les valeurs absolue. Normalement l'intersection de A et B devrait donner les deux points cités plus haut

Remarque: Vu le niveau des olympiades en général, ma solution me parait un peu simple. J'aimerai bien que quelqu'un de plus calé la valide

a+

[yos]

E(x)+E(y)=1 alors forcement soit (x,y)=(0,1) soit (x,y)=(1,0)

"forcément"... C'est bien une question de force.

[rene38]

E(x)+E(y)=1 alors forcement soit (x,y)=(0,1) soit (x,y)=(1,0)

et pourtant et

[yos]

Pour la première équation, tu distingues les 4 cas correspondants aux 4 quadrants du repère. Par exemple l'intersection de A avec le quadrant 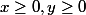a pour équation x²+y²=1. C'est donc le quart de cercle de centre O, de rayon 1 contenu dans ce quadrant. Dans le quadrant , l'équation est x²-y²=1, donc partie d'hyperbole.. Dans le quadrant , c'est le symétrique de la portion d'hyperbole précédente par rapport à la droite d'équation y=x. Dans le quatrième quadrant, il n'y a rien. N'oublie pas que la courbe est continue malgré les 3 morceaux.
Pour la seconde équation, tu ne découpes plus le plan en quadrant mais en bandes verticales , où k est un entier. Dans une telle bande, on a E(x)=k et on cherche donc les points (x,y) tels que E(y)=1-k, c'est-à-dire . On obtient donc un petit carré de côté 1 dans chaque bande.
Fais le dessin!

[aviateurpilot]

c'est un exo olympiad

x|x|+y|y|=1
x,y>0 donne , S1={(sina,cosa)\a de R}
x,y0 et y0 S3={()}

E(x)+E(y)=1
S={}

pour x|x|+y|y|=1 c'est tres facile (un cercle ,.......)

pour E(x)+E(y)=1