slt
j'ai besoin d'aide dans cet exercice
pour n de N* fixé. on pose Zn=exp(2i/n)
1-calculer selon r de Z la valeur de
n-1
;) (Zn)puissance kr ""le resultat c 0""
k=0
2- pour tt n de N* on pose
n-1
Gn= ;) (Zn)puissance k²
k=0
a-montrer que pour j de N on a
n-1 Gn= ;) (Zn)puissance (k+j)²
k=0
on poura poser j=nq+r
b-montrer que si n est un entier impair alors Gn.Gn¯ =n
c-monter Gn=(1+ipuissance-n)(racine n)/(1+ipuissance-1)
calculer Gn si n=1 modulo 4 et si n=3modulo4
svp donner moi de sugestions et des idees
Suite et sommation
5 messages
- Page 1 sur 1
selon les valeurs de k on calcule la somme
on a 2 cas
si n divise r (dans le cas de n=1) alors c'est 1
si n ne divise pas r alors c'est o
c'est ma faute j'ai parlé just du cas general
pour qustion 2
pour tt n de N* on pose
n-1
;) ((Zn)^ k²) = Gn
k=0
a-montrer que pour j de N on a
n-1
;) ((Zn)^ (k+j)²) = Gn
k=0
(on poura poser j=nq+r)
b-montrer que si n est un entier impair alors Gn.Gn¯ =n (Gn¯ signifie le conjugue de Gn)
c-monter Gn=(1+(i^-n))(racine carée de n) / (1+(i^-1))
calculer Gn si n=1 modulo 4 et si n=3modulo4
on a 2 cas
si n divise r (dans le cas de n=1) alors c'est 1
si n ne divise pas r alors c'est o
c'est ma faute j'ai parlé just du cas general
pour qustion 2
pour tt n de N* on pose
n-1
;) ((Zn)^ k²) = Gn
k=0
a-montrer que pour j de N on a
n-1
;) ((Zn)^ (k+j)²) = Gn
k=0
(on poura poser j=nq+r)
b-montrer que si n est un entier impair alors Gn.Gn¯ =n (Gn¯ signifie le conjugue de Gn)
c-monter Gn=(1+(i^-n))(racine carée de n) / (1+(i^-1))
calculer Gn si n=1 modulo 4 et si n=3modulo4
Le code pour écrire en mode maths n'est pas très compliqué.
Pour la somme par ex tu fais
qui donne
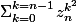
A partir du niveau BAC +1 c'est très pratique pour lire.
Pour la somme par ex tu fais
- Code: Tout sélectionner
\Sigma_{k=0}^{k=n-1}z_{n}^{k^{2}}
qui donne
A partir du niveau BAC +1 c'est très pratique pour lire.
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
