Suite

[soffie]

bonjour alors j'ai un problème avec un exercice sur les suites:
l'ènoncé: = -
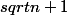
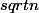
etudier le sen de variation de Un
mon travaille:je fais Un+1 - Un donc
- - +
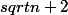
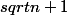
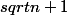
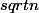
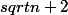
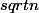
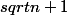
après développement je trouve + -2 et la je bloque

[girdav]

Bonjour.
Tu peux, si tu ne veux pas t'embrouiller avec le signe de et travailler avec telle que .

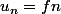[maturin]

oui le plus simple c'est d'étudier la fonction f(x)=rac(x+1)-rac(x)

maintenant tu peux dire:
rac(n+2)+rac(n)-2rac(n+1)<0
ssi rac(n+2)+rac(n)<2rac(n+1)
ssi n+2+n+2rac(n(n+2))<4(n+1) -- j'ai pris le carré et les nb sont positifs
ssi 2rac(n(n+2))<2(n+1)
ssi 4n(n+2)<4(n+1)²
ssi n(n+2)<(n+1)²
ssi 0<1

[soffie]

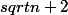
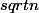
merci pour ta réponse mais ^2+ ^2=n+2+n+2
je comprend pas se calcul parce que moi quand je fais tous au carrè je trouve n+2+n

[maturin]

il faut faire ce qui est de la forme (a+b)²=a²+b²+2ab

tu as le droit de mettre au carré chaque côté de ton inégalité sans changer le signe si tes nombres sont positifs

par contre mettre au carré chaque membre d'une addition c'est n'importe quoi