[1ère S] fonctions polynômes

[Ferterps]

Bonsoir,

Je ne comprend absolument cet exercice : voici tout d'abord l'énoncé:

>

Je sais qu'un polynôme du degré 2 est sous la forme mais ici on a aucune racine, aucun indice qui nous permette de trouver le polynôme.

ai-je mal compris l'énoncé ? faut il trouver une valeur ?

Merci beaucoup

[HanZel]

Oui, en fait donc tu bidouilles un peu ton x en x+1 à l'interieur du polynome, tu fais la difference dans ton équation et tu vois ce qui se passe :happy2: .
Ensuite la question est de trouver un polynome, donc tu cherches un triplet (a,b,c) qui marche.

[Ferterps]

Merci de ta réponse, je trouve a = 1/2 et b = -1/2 et c = 2 ça marche mais j'ai trouver ces valeurs en remplaçant x par 2 puis 3 pour obtenir un système à 2 incongrues que j'ai résolu, mais j'ai trouvé ça au petit bonheur la chance, alors je ne sais pas comment rédiger (pour un DM) ou alor trouver une autre alternative ? merci

[HanZel]

Quand tu fais soit , il est censé te rester une équation "normale" sans avec et .

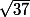
Ton équation obtenue, tu sais qu'elle doit être valable quelque soit la valeur de x, donc en particulier pour x=2 et x=3 comme tu as choisi. (Tu aurais pu prendre et si tu avais voulu)

Tu vois au passage que tu n'as plus de (ce qui veut dire que c peut prendre n'importe qu'elle valeur réelle...).

Donc en conclusion tu as tiré un polynôme (une solution comme demandé dans la question).
Mais tu peux aussi donner la totalité de l'ensemble de ces polynômes : "L'ensemble des polynômes P verifiant l'équation... est du type :"

Pour ta rédaction, ton "petit bonheur la chance" tu le justifies par le fait que c'est valable pour tout x (je suppose que c'est dans R) et que par conséquent, tu as le droit d'en choisir 2 comme tu veux (fait au plus simple, par exemple 0 et 1 t'auras encore moins de calculs!)

J'espère que ça ira avec ça

[Ferterps]

Merci Hanzel, j'ai fini de rédiger je vous met la suite qui est d'une stupidité ... :

>

alors déjà en premier l'égalité précedente, c'est celle que j'ai trouvé moi ou celle donnée ? ?
ET je trouve ça évidemment, enfin je vois pas qu'est ce qu'il faut chercher ?

merci beaucoup

[HanZel]

Il y a deux parties dans la question:
1) écrire
2) calculer

1) Il faut que tu écrives ces égalités :
x=1 : P(2)-P(1)=1
x=2 : P(3)-P(2)=2
...
x=n : P(n+1)-P(n)=n

tu as juste remplacé le x par 1,2,3...,n
(Oui bien sur tu trouves que ça marche, là question que tu as fais juste avant sert à trouver P pour que ça marche).

2) Tu dois trouver ce que vaut 1+2+3+...+n avec les égalités du dessus, ce qui est (P(2)-P(1)) + (P(3)-P(2)) +...+ P(n+1)-P(n)= 1+2+3+...+n
Tu simplifies à gauche de l'égalité et tu changes tes P(x) par (1/2)x²-(1/2)x, tu développes, tu simplifies, tu factorises et ton résultat vaut 1+2+3+...+n

[Ferterps]

merci beaucoup hanzel ça a marché :) je te remercie beaucoup.

[Malezan]

Soit P un polynome de degré 4. On pose:
P(x)=ax(x est puissance 4)+bx(x est au cube)+cx²+dx+e
ou a b c d e sont des nombres reels.
Sachant que
- le terme constant de P vaut 10
- il n'y a pas de monome de degré 2
- P(1)=24
- P(-1)=0
- P(2)=0
Determiner P(x)

Je suis arrivé à P(x)=ax4+bx3+dx+10
Et là... Bloqué!
Si vous pouviez m'aider... :)

PS: Mes chiffres aprés mes x sont des puissances, c'est parce que je sais pas les faire a part x² :/