Bonjour, je dois rendre un DM ce lundi et je bloque déja !!
Voici l'exercice :
z=x+iy
on pose Z=(1+z)(i+zbar)
a) déterminer et représenter l'ensemble E des points M d'affixe z tels que Z soit réel.
b) Déterminer et représenter l'ensemble F des points M d'affixe z tels que Z soit imaginaire pur.
J'ai donc calculer Z et je trouve Z=x²+y²+x-y+i(1-y+x)...et la je suis bloqué, je n'arrive pas a déterminer x et y, j'ai besoin de votre aide !!
Un grand merci à tous.
DM Complexes
6 messages
- Page 1 sur 1
re,
je te montre en calcul intrinsèque (sans coordonnées) :id:
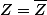
la conjugaison est un morphisme de corps, toutes les opérations passent
au conjugué:
(i+\bar{z})=(1+\bar{z})(-i+z))
on développe (on est dans un anneau)

on regroupe
- \bar{z} (-1-i)+2i=0)
on va voir sur l'ile-aux-maths, ce que l'on a obtenu
est pile-poil une équation de droite en complexe :id:
lire içi
je te montre en calcul intrinsèque (sans coordonnées) :id:
la conjugaison est un morphisme de corps, toutes les opérations passent
au conjugué:
on développe (on est dans un anneau)
on regroupe
on va voir sur l'ile-aux-maths, ce que l'on a obtenu
est pile-poil une équation de droite en complexe :id:
lire içi
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
