bonjour,
Voici mon problème
Je résous l équation de deux façons et je narrive pas aux mêmes conclusions.
Racine(x)+x = 0
Je suis en première S
Méthode 1
Racine(x) ( 1+racine(x)) =0
Donc x=0 ou 1+racine(x) = 0 ce qui est impossible
Donc il y a une seule solution x=0
Méthode 2
Racine(x)= -x
(Racine(x)) ^2 = (- x)^2
x = x^2 ( car x>=0)
x^2-x =0
x (x-1) =0
donc x=0 ou x=1
or 1 nest pas solution de léquation de départ !!
je vois bien que que la ligne racine(x) = - x nest pas possible puisque x doit être positif ou nul et quune racine est aussi positive ou nulle.. et que cest sûrement de la que vient le problème.
Pourtant cette ligne vient de léquation donnée
Merci
X+racine(x)=0
11 messages
- Page 1 sur 1
bj,
en élevant au carré, on introduit une solution parasite,
solution , égale à 1, de l'équation
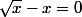
les deux équations E_1 et E_2 ne sont pas équivalentes, auquel cas elles aurait les mêmes solutions.
simplement l'équation implique l'équation
implique l'équation 
et dans ce cas l'ensemble des solutions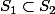
ie, toute solution de l'équation est solution de l'équation
est solution de l'équation 
E1: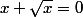
E2: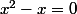
en élevant au carré, on introduit une solution parasite,
solution , égale à 1, de l'équation
les deux équations E_1 et E_2 ne sont pas équivalentes, auquel cas elles aurait les mêmes solutions.
simplement l'équation
et dans ce cas l'ensemble des solutions
ie, toute solution de l'équation
E1:
E2:
je suis d'accord avec ce que dit echevaux mais dans mon cas je raisonne dès le départ sur des nombres positifs ou nuls. puisque l'ensemble de définition de l'équation dépend de la racine carrée.
or sur les positifs on a l'équivalence :
si deux nombres au carré sont égaux alors ces nombres sont égaux !!
on a donc l'équivalence !
donc on a pas du tout ce problème de nombres opposés.
et je ne comprend pas du tout pourquoi le fait d'élever au carré introduit une solution parasite puisque encore une fois on garde l'équivalence en raisonnant sur des positifs !!
or sur les positifs on a l'équivalence :
si deux nombres au carré sont égaux alors ces nombres sont égaux !!
on a donc l'équivalence !
donc on a pas du tout ce problème de nombres opposés.
et je ne comprend pas du tout pourquoi le fait d'élever au carré introduit une solution parasite puisque encore une fois on garde l'équivalence en raisonnant sur des positifs !!
racine (1)+1=0 est faux
racine(1)= -1 est faux
maintenant si tu élèves au carré cela devient vrai.
donc c'est bien en passant au carré ton égalité que tu fais rentrer une solution qui existe vraie au carré et est fausse quand pas au carré.
c'est ce qui t'es dit depuis le début,
rends toi t'es cerné :we:
racine(1)= -1 est faux
maintenant si tu élèves au carré cela devient vrai.
donc c'est bien en passant au carré ton égalité que tu fais rentrer une solution qui existe vraie au carré et est fausse quand pas au carré.
c'est ce qui t'es dit depuis le début,
rends toi t'es cerné :we:
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
