Bonsoir tout le monde!
Je suis en prépa BCPST (Agro-véto) et j'ai un exercice à faire sur la trigo:
Résoudre dans RxR le système suivant:
x+y = 5 pi /12
sinx + siny = 1/2 + V3/2
Alors j'ai trouvé que
sinx + siny = sin(pi/6) + sin(pi/4).
Si on remplace x par pi/6 et y par pi/4 ou vice-versa, la première équation est vérifiée, cela semble être la bonne réponse.
Mais je me posais la question de savoir si on peut identifier si "facilement" les 2 côtés de l'équation n° 2 (sinx + siny = 1/2 + V2/2)?!
Y a t'il une justification particulière à donner ou faut-il passer un tout autre chemin?
Merci d'avance!
Résolution d'un système avec des sinus
6 messages
- Page 1 sur 1
bonjour,
intéressant.
il y a une solution évidente:
le couple=(\frac{\pi}{6},\frac{\pi}{4}))
ensuite, on soustraie membres
à membres les deux systèmes) et
et )
pour se débarrasser des constantes à droite des égalités.
après bidouillage (formules de Simpson ) , tu peux te ramener à la
réunion de plusieurs systèmes linéaires 2x2 de Cramer, d'inconnues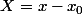 et
et 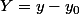
intéressant.
il y a une solution évidente:
le couple
ensuite, on soustraie membres
à membres les deux systèmes
pour se débarrasser des constantes à droite des égalités.
après bidouillage (formules de Simpson ) , tu peux te ramener à la
réunion de plusieurs systèmes linéaires 2x2 de Cramer, d'inconnues
BreakingDawn a écrit:bonsoir, merci pour ta réponse,
mais je ne vois pas bien ce que sont les systèmes linéaires 2x2 de Cramer, n'ayant encore jamais vu ça en cours.
bah si (programme de seconde)
peux-tu écrire le système général d'inconnues x,y
et le système particulier vérifié par le couple
ensuite, on soustraie. les constantes s'en vont. :id:
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
