Développer expression racines carrés

[amaze]

Salutation.

J'ai donc un problème, le voici :

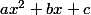
Sachant que p(x)= et ses racines x1 et x2 tel que
x1= et x2=

Montrer que

Je dois donc montrer que :

Le problème est que je ne vois pas comment développer cette expression (tout ce qui est avant le "="). De plus, je ne me rappelle plus si j'ai le droit de simplifier ce qu'il y a dans les racines de cette sorte (par exemple (le 4 en haut et le 4 en bas s'annulent)...

Pouvez-vous m'aider s'il vous plait ?

[L.A.]

Bonjour.

La propriété à utiliser est : (a/b)*(c/d) = (ac)/(bd)

avec un peu d'huile de coude on y arrive.

ne veux tu pas dire (4*2)/4 = 2 ?

[amaze]

L.A. -> Exacte, j'ai fait une faute de frappe, (4*2)/4 est bien égal à 2

J'ai donc essayé de développer mais le problème c'est que je trouve comme résultat final à la place de .

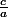
Est-ce que les "-" juste avant les racines doivent être distribuer à toute la racine ? :/

[L.A.]

Oui, enfin, le moins ne peut pas "rentrer" dans la racine.
mais par exemple -(V(a+b))² = -(a+b) = - a - b

Un moyen déviter les erreurs au brouillon : Pose A= -b , B = V(b²-4ac)
et utilise une id. remarquable pour la forme (A-B)(A+B) du numérateur.

[oscar]

Bonsoir s = ( -b - v(b²-4ac)/2a) ( -b+v( b² - 4ac)/2a) =
Formule( A-B)(A+B)=A² - B²
s = (-b)² - (v(b²-4ac)²/ 4a²= b²- b² +4ac)/4a²= 4ac/4a²= c/a

[Cornelius]

Oui il y a une identité remarquable