Trois questions simples sur les complexes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
jacky.C
- Membre Naturel
- Messages: 26
- Enregistré le: 09 Sep 2009, 15:00
-
 par jacky.C » 16 Sep 2009, 08:38
par jacky.C » 16 Sep 2009, 08:38
bonjour, merci de m'indiquer quelques pistes pour que j'arrive à répondre à ces questions .... :)
Q1) l'ensemble des points M d'affixe z vérifiant !-2iz+1-4i!=4 (! pour les barres de valeur absolue):
un cercle de centre (-2;-05), un cercle de centre (-1,5;-05), un cercle de rayon 3, un cercle de rayon 2,5, une droite ?
Q2) l'ensemble des point M d'affixe z vérifiant !z-1!=!z-i! :
un cercle, une droite y=x, une droite passant par A(2;1,5), la droite y=2x, la droite y=x+1 ?
Q3) je n'arrive pas à trouver aussi l'argument de (Rac(3)+i)^5:
Cos O= Rac(3)/32 et Sin O= 1/32 donc O= ... ?
Merci d'avance !
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 16 Sep 2009, 08:43
par girdav » 16 Sep 2009, 08:43
Bonjour.
Dans les deux cas pose
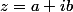
et réécris les équations avec ça.
-
jacky.C
- Membre Naturel
- Messages: 26
- Enregistré le: 09 Sep 2009, 15:00
-
 par jacky.C » 16 Sep 2009, 08:50
par jacky.C » 16 Sep 2009, 08:50
Oui, c'est déjà fait mais aprés ? je ne vois pas bien dans quelle direction je dois aller, sur quoi je dois tomber ...
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 16 Sep 2009, 08:55
par girdav » 16 Sep 2009, 08:55
Pour la première:
+1-4i \right|=\left|-2ia-2i^2b+1-4i \right|<br />=\left|-2ia+2b+1-4i \right| =\left|2b+1-4i-2ia \right|=\left|2b+1-2i\(a+2\) \right| =\sqrt{\(2b+1\)^2+4\(a+2\)^2})
-
jacky.C
- Membre Naturel
- Messages: 26
- Enregistré le: 09 Sep 2009, 15:00
-
 par jacky.C » 16 Sep 2009, 09:09
par jacky.C » 16 Sep 2009, 09:09
Et maintenant comment savoir si c'est un cercle ou une droite ? :hein:
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 16 Sep 2009, 09:12
par girdav » 16 Sep 2009, 09:12
On a que la racine de "tout ça vaut

. Il faut éléver au carré pour savoir.
-
jacky.C
- Membre Naturel
- Messages: 26
- Enregistré le: 09 Sep 2009, 15:00
-
 par jacky.C » 16 Sep 2009, 09:27
par jacky.C » 16 Sep 2009, 09:27
Merci beaucoup j'ai trouvé pour la Q1, un cercle de centre (-2;-0,5) et de rayon 2 !
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 16 Sep 2009, 09:39
par girdav » 16 Sep 2009, 09:39
Il faut procéder de même pour la question 2).
Pour la 3), on a que
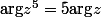 \[2\pi\])
grâce au lien entre produit et argument.
Reste à trouver celui de

. Pour cela, calcule le module et mets le en facteur. Tu devrais voir le truc.
-
jacky.C
- Membre Naturel
- Messages: 26
- Enregistré le: 09 Sep 2009, 15:00
-
 par jacky.C » 16 Sep 2009, 09:49
par jacky.C » 16 Sep 2009, 09:49
Pour la Q2) je trouve 2(b-a)=0, c'est l'équation d'une droite ? :hum:
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 16 Sep 2009, 09:55
par girdav » 16 Sep 2009, 09:55
Oui, en fait on a

en simplifiant par deux donc la partie réelle est égale à la partie imaginaire.
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 16 Sep 2009, 10:49
par abcd22 » 16 Sep 2009, 10:49
Bonjour,
jacky.C a écrit:(! pour les barres de valeur absolue):
Tu peux utiliser le caractère « | » qui est sur AltGr-6 sur les claviers AZERTY français (même si sur beaucoup de claviers le caractère affiché sur la touche est « ¦ ».
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 16 Sep 2009, 10:57
par yos » 16 Sep 2009, 10:57
Et

c'est pareil que
|)
(mettre -2i en facteur dans le module).
C'est donc la distance AM où M(z) et
)
.
-
mathelot
 par mathelot » 16 Sep 2009, 12:10
par mathelot » 16 Sep 2009, 12:10
bonjour,
pareil pour la question 2
|z-1| est la distance M(z) au point A(1)
|z-i| est la distance M(z) au point B(i)
La distance de M aux points A et B est la même.
on obtient donc ...
pour la dernière question, écrire le nombre complexe

sous forme trigo

est alors immédiatement sous forme trigo
a priori
=\frac{5\pi}{6})
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
