Applications, Fonctions polynomes 1°S

[Peau de Peche]

Bonjour, je suis actuellement en 1°S et j'ai un exercice sur lequel je sèche complètement :triste: ! Pouvez vous m'aidez ?

Voici l'énoncé :

Soit P(x) = 1/24 ( x^4 - 2x^3 + 11x^2 + 14x + 24 ) ; Peut-on affirmer que, pour tout n ;) N , P(n) = 2^n ?


Merci, C.

[Ferterps]

n signifie quoi ? la puissance ? la racine ? x ?

[Peau de Peche]

n Représente un naturel.

[Ericovitchi]

Bien sûr que non, ça n'est vrai que pour n variant de 0 à 4, à partir de 5 ça devient faux.

[Peau de Peche]

Daccord, mais pourquoi ? ( le raisonnement m'interesse beaucoup plus que la reponse :we: )

[badmooove2]

ja sais je dois pas faire dla pub pour ma discut mais qqlun peut m'aider pour la chimie svp c'est simple

[Ericovitchi]

En fait s'il existait un polynôme ayant un nombre fini de termes tel que 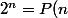, ça voudrait dire que la fonction exponentielle (car ) s'exprime sous la forme d'un polynôme or la fonction exponentielle est définie de manière unique par la série infinie , on voit bien que cette serie ne peut être égale à un polynôme ayant un nombre fini de termes.

Donc forcement il existe un n ou va ne plus être égale à P(n) et ceci quelque soit le polynôme.
Dans le cas présent pour ajouter à la confusion on a choisi un polynôme qui a des valeurs qui marchent jusqu'à n=4 mais à n=5 l'illusion tombe.

[Peau de Peche]

Daccord ! Merci :we: ! Cependant je ne vois pas comment j'aurais pu trouver etant donner que nous avons pas encore parler des fonctions exponentielle =S Merci a toi :) bizoow

[Ericovitchi]

moi franchement, j'ai pris mon tableur préféré, j'ai rentré l'équation, je l'ai calculé pour n allant de 1 à 20 et j'ai immédiatement vu que pour n supérieur à 5 ça ne marchait plus.

les méthodes bestiales ça marche aussi.

[Peau de Peche]

Hann Oui, J'aurais jamais penser a faire ça, tu vois ^^ :++:

[Peau de Peche]

Tya utiliser quoi enfaite ? ta fait =SI( etc... ??