Combinaisons, sommes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
gilles3
- Membre Naturel
- Messages: 26
- Enregistré le: 18 Avr 2009, 18:41
-
 par gilles3 » 15 Sep 2009, 16:28
par gilles3 » 15 Sep 2009, 16:28
Bonjour, j'ai un exercice à faire, mais je ne vois pas du tout comment faire:
Soit

un entier naturel non nul.
Exprimer de deux façons suivantes
^{2m})
pour calculer:
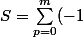^p C_{2m}^{2p}})
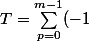^p C_{2m+1}^{2p}})
.
J'ai pensé à calculer d'abord
^m=\displaystyle{\sum_{p=0}^m C_m^p i^p})
, mais si on élève le tout au carré, je vois pas trop comment s'en sortir:
^{2m}=\displaystyle{\left(\sum_{p=0}^m C_m^p i^p\right)^2})
, expression qu'on ne peut pas développer.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 15 Sep 2009, 16:34
par Nightmare » 15 Sep 2009, 16:34
Salut !
Et pourquoi pas tout simplement :
^{2m}=\Bigsum_{p=0}^{2m} C_{2m}^{p} i^{p})
?
Pour la deuxième manière, je suggérerai de développer (1+i)² et après d'utiliser le binôme de Newton.
-
gilles3
- Membre Naturel
- Messages: 26
- Enregistré le: 18 Avr 2009, 18:41
-
 par gilles3 » 15 Sep 2009, 16:37
par gilles3 » 15 Sep 2009, 16:37
Alors
^{2m}= \displaystyle{\sum_{k=0}^{2m} C_{2m}^k i^k})
Si k est pair, alors k=2p, p entier naturel et
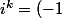^p)
Si k est impair, alors k=2p+1, et
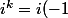^p)
Donc
^{2m}= \sum_{p=0, p \text{pair}}^{2m} C_{2m}^{2p} (-1)^p+i \sum_{p=0, p \text{impair}}^{2m} C_{2m}^{2p+1} (-1)^p})
et là je n'obtient pas

-
gilles3
- Membre Naturel
- Messages: 26
- Enregistré le: 18 Avr 2009, 18:41
-
 par gilles3 » 15 Sep 2009, 16:38
par gilles3 » 15 Sep 2009, 16:38
Ah si on obtient bien

.
Je vois pas trop comment claculer de la deuxième manière.
-
gilles3
- Membre Naturel
- Messages: 26
- Enregistré le: 18 Avr 2009, 18:41
-
 par gilles3 » 15 Sep 2009, 16:41
par gilles3 » 15 Sep 2009, 16:41
si je calcule
^2 =2i)
je vois pas trop comment appliquer la formule du binôme de Newton pour
^m)
.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 15 Sep 2009, 16:54
par Nightmare » 15 Sep 2009, 16:54
On en a pas besoin comme tu le vois, on a directement le résultat : 2^m i^m. Identifie ensuite partie imaginaire et partie réelle pour en déduire la valeur de S et celle de T.
-
gilles3
- Membre Naturel
- Messages: 26
- Enregistré le: 18 Avr 2009, 18:41
-
 par gilles3 » 15 Sep 2009, 17:05
par gilles3 » 15 Sep 2009, 17:05
autrement dit, j'ai:
comme

pair, on a alors
^{2m}=2^m i^m=2^m(-1)^{m/2})
, avec

entier naturel, donc
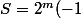^{m/2})
et
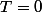
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 15 Sep 2009, 17:14
par Pythales » 15 Sep 2009, 17:14

...
-
gilles3
- Membre Naturel
- Messages: 26
- Enregistré le: 18 Avr 2009, 18:41
-
 par gilles3 » 15 Sep 2009, 17:31
par gilles3 » 15 Sep 2009, 17:31
j'ai pas trop compris la remarque:
autrement dit, on aurait
^2=2e^{i\frac{\pi}{2}})
donc
^{2m}=2^m e^{i\frac{\pi}{2}m}=2^m \cos \frac{\pi}{2}m + i 2^m \sin frac{\pi}{2}m= 2^m \cos \frac{\pi}{2}m + i 2^m \sin \frac{\pi}{2}m)
.
Donc

et

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités