Equation

par **Anonyme** » 19 Fév 2006, 17:33

j'ai f(x)=(x^3+x²+1)/(9x²)

f'(x)=(3(2x^3+x²-1))/((9x²)²)

et je voudrai savoir les variation de f(x) sur R*

merci d'avance

par **usul** » 19 Fév 2006, 17:50

es-tu sur de ta dérivé je trouve (x^3-2)/(9x^3)

par **leibniz** » 19 Fév 2006, 17:51

Salut,

Tu es sûr de ta dérivée?

A+

par **leibniz** » 19 Fév 2006, 17:51

Réponses croisées!

par **usul** » 19 Fév 2006, 17:53

les grands esprits se rencontrent

par **Anonyme** » 19 Fév 2006, 17:59

je pense que oui car il y a une question dans ce même exercice et il faut étudié 2x^3+x²-1 , et c'est mon probleme je ne sais plus comment il faut faire...

par **allomomo** » 19 Fév 2006, 18:45

Salut,

par **lomdefer** » 19 Fév 2006, 18:49

USULE a raison, la dérivée est bien : f'(x) =x^3-2/9x^3

Ben pour savoir la variation de f(x) sur R il faut que tu étudie le signe de f'(x) :

X^6-2>=0 pour x>= (2^(1/3))^3 (racine cubique de 2)
9x^3>=0 pour x>= 0

Donc de - infini à 0 f'(x) est >0 donc f(x) est croissant, de 0 à racine cubique de 2 f'(x) est <0 donc f(x) est décroissant et de racine cubique de 2 à + l'infini f'(x) est >0 donc f(x) est croissant.
Voila

Au plaisir

par **alyssa** » 19 Fév 2006, 19:05

Quelqu'un pourrait il m'aider, je suis désespérée. Mon nom est alyssa et mon énoncé concerne les fonctions et la géométrie niveau seconde. Merci d'avance.

par **leibniz** » 19 Fév 2006, 19:07

allomomo a écrit:Salut,

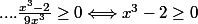
Tu es sûr de cette équivalence?

par **allomomo** » 19 Fév 2006, 19:19

Salut leibniz,

Corrige moi si je me trompe :

Si c'est pas ca, alors c'est ca :

par **alyssa** » 19 Fév 2006, 19:22

Aide moi allomomo

par **leibniz** » 19 Fév 2006, 19:23

C'est une inégalité, donc il faut faire attention au signe lors de la multiplication......
a+

par **allomomo** » 19 Fév 2006, 19:25

ils sont tous positifs

par **leibniz** » 19 Fév 2006, 19:27

Qui sont tous positifs??? Je parle de 9x^3 qui le mêùe signe de x donc si x est négatif.....

A+

par **Anonyme** » 19 Fév 2006, 19:29

est-ce que f(x) = 1/3(x²+x+1/x) = (x^3+x²+1)/(9x²) ???

j'ai l'impression de mettre trompé

par **leibniz** » 19 Fév 2006, 19:32

kikou a écrit:est-ce que f(x) = 1/3(x²+x+1/x) = (x^3+x²+1)/(9x²) ???

j'ai l'impression de mettre trompé

Tu veux dire quoi? Cette derniere égalité est fausse bien sûr!

par **lomdefer** » 19 Fév 2006, 19:32

oui tu t'es trompé car 1/3*(x^2+x+1/x)=(x^3+x^2+1)/3x

par **leibniz** » 19 Fév 2006, 19:33

Qui s'est trompé???!!!

par **lomdefer** » 19 Fév 2006, 19:35

kikou...dsl j'ai pas préciser

Equation

equation

Qui est en ligne