Intégrale avec variable dans une borne
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
nicos13
- Membre Naturel
- Messages: 22
- Enregistré le: 12 Sep 2006, 20:33
-
 par nicos13 » 13 Sep 2009, 13:35
par nicos13 » 13 Sep 2009, 13:35
Bonjour,
Je dois trouver dans un exercice d'électrostatique la charge totale d'une calotte sphérique. Pour cela je dois calculer une triple intégrale, (je passe les détails) et le résultat est le suivant :
}{ dz)
(La formule est certaine, je suis allé voir le prof et il m'a confirmé que c'était bien la bonne)
où theta est l'angle sous lequel est vu le disque fermant la calotte et R le rayon de la sphère qui engendre la calotte.
Le problème est que je dois intégrer r.dr mais qu'une des bornes contient une variable ( z ). Apparemment le prof a dis qu'il fallait faire un changement de variable mais je vois vraiment pas comment faire...
Merci de votre aide si vous voulez plus de précisions je mettrai l'énonce avec le schéma.
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 13 Sep 2009, 13:55
par abcd22 » 13 Sep 2009, 13:55
Bonjour,
nicos13 a écrit:}{ dz)
L'intégrale est donc
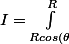 \(\int^{\sqrt{R^2-z^2}}_{0} \(\int^{2\pi}_{0} d\phi\) r.dr\) dz)
, on n'a pas le droit de séparer les intégrales en trois comme tu l'as écrit car comme tu l'as remarqué, quand on intègre suivant r on trouve quelque chose qui dépend de z et qu'on va donc intégrer de nouveau après. Ici on peut seulement sortir l'intégrale en phi qui est indépendante des autres, ce qui donne :
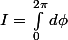 \(\int^R_{Rcos(\theta) \(\int^{\sqrt{R^2-z^2}}_{0} r.dr\) dz\))
, qu'on calcule en calculant d'abord l'intégrale en r (et celle en phi puisqu'elle est facile), puis celle en z.
-
nicos13
- Membre Naturel
- Messages: 22
- Enregistré le: 12 Sep 2006, 20:33
-
 par nicos13 » 13 Sep 2009, 14:12
par nicos13 » 13 Sep 2009, 14:12
a ok, c'est tout nul en fait...
J'ai l'habitude de séparer les variables à chaque fois qu'il y a une triple intégrale et c'est vrai que la c'est pas possible je comprends mieux pourquoi j'y arrivais pas merci en tout cas...
Le résultat donne donc si je me trompe pas :
 + (1/3)cos^3(\theta)))
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
