Récurrence terminale S

par **wallen22** » 12 Sep 2009, 16:53

Bonjour !! tu es nouveau sur le forum: je t'invite à aller lire d'urgence le réglement!je me retrouve avec de nouveau à DM à rendre, et encore une fois j'ai droit à un exo sur la récurrence et j'ai un peu de mal avec ça.

Alors voilà l'exo:

Pour tout entier naturel n on pose Sn= (1/(1*2*3)) + (1/(2*3*4)) + ..... + 1/ [(n(n+1)(n+2)]
Etablir par récurrence : pour tout n appartenant à N* Sn= [n(n+3)]/ (4(n+1)(n+2) ]

alors j'ai réussi l'étape de l'initialisation mais quelle galére pour l'hérédité!

alors voilà ce que j'ai pour l'hérédité:

k appartient à N* je suppose que P(k) est vraie.

(1/(2*3*4)) + ..... + 1/ [(k(k+1)(k+2)] = [k(k+3)]/ (4(k+1)(k+2) ]

je sais que je dois montrer que
(1/(2*3*4)) + ..... + 1/ [(k+1)(k+1+1)(k+1+2)] =[(k+1)(k+3)]/ (4(k+1+1)(k+1+2) ]

J'ai donc ajouté à (1/(2*3*4)) + ..... + 1/ [(k(k+1)(k+2)] = [k(k+3)]/ (4(k+1)(k+2) ]
de chaque coté 1/ [(k+1)(k+2)(k+3)]

je réduis au même dénominateur j'obtiens :

[ k(k+1)(k+4)k+1)(k+2)(k+3)+4(k+2)(k+3)] / [4(k+2)(k+3)(k+1)(k+2)k+3) ]

mais je fais quoi avec tout ça si je développe tout le numérateur ça me donne un truc hyper long avec lequel je parviens pas à prouver ce que je veux!

par **fatal_error** » 12 Sep 2009, 17:27

salut,

une astuce :
Tu as

Soit

soit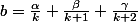

On va essayer de trouver les coefficients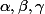

, tels que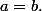

Supposons qu'ils existent.
donc on pose

.
Maintenant on multiplie des deux cotés par k.

.
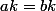Puis, on va evaluer si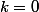

. Soit doit permettre de trouver

.
Ensuite on fait

et on evalue pour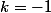

, ce qui permet de trouver

Enfin, idem pour

.

Une fois qu'on a les trois coeff (ca sappele decomposition en fraction rationnelle), et va pouvoir ecrire notre somme de terme

, et on a des termes qui vont alors sauter.

par **wallen22** » 12 Sep 2009, 19:48

euh... il n'y aurait pas plus simple ? tout en restant dans le principe de la récurrence ?
je m'y perd trop là.

par **girdav** » 12 Sep 2009, 19:56

Bonjour.
En fait tu as à arranger

Tu as un facteur commun:

. Le calcul est plus facile.

par **wallen22** » 12 Sep 2009, 20:06

Sauf que moi j'en suis là : à la supposition que p(k) est vrai, :

[ k(k+1)(k+4)k+1)(k+2)(k+3)+4(k+2)(k+3)] / [4(k+2)(k+3)(k+1)(k+2)k+3) ]

par **girdav** » 12 Sep 2009, 20:08

Oui, en fait j'ai pris

au lieu de

. Mais sinon ça allège les calculs.

par **wallen22** » 12 Sep 2009, 20:13

j'y arrive pas je ne peux rien simplifier! ça me donne des k^3 voir k^5 enfin bref c'est compliqué!!!!!

par **girdav** » 12 Sep 2009, 20:23

Attends, on va faire le calcul tranquillement. On a

et tu remarques que le dénominateur admet

pour racine.

par **wallen22** » 12 Sep 2009, 20:32

ok mais à quoi sert tout ça quand je veux parvenir à p(k+1) est vrai ?
et pourquoi préciser -1 est une racine .?

par **girdav** » 12 Sep 2009, 20:33

Parce que tu peux factoriser par

.

par **wallen22** » 12 Sep 2009, 20:36

vous vouliez pas plutot dire que -1 est racine du numérateur ? plutot que dénominateur ?

par **girdav** » 12 Sep 2009, 20:39

C'est vrai pour les deux, mais le fait que tu l'ai remarqué montre que tu es sur la bonne voie!

par **wallen22** » 12 Sep 2009, 20:45

oui mais comment factoriser? moi j'arrive à factoriser des polynomes de second degré pas du troisième! à moins de diviser le numérateur par (k+1)

par **wallen22** » 12 Sep 2009, 20:47

ce qui donne pour le numérateur (k+1)(k²+5k+4)
mais le dénominateur je ne sais pas comment le factoriser.

par **wallen22** » 12 Sep 2009, 20:49

d'aillleurs j ene comprend pas quand vous me dites que -1 est racine du dénominateur.
car 4(-1+1)*(-1+2)*(-1+3) donne pas 0 .

par **girdav** » 12 Sep 2009, 20:53

wallen22 a écrit:d'aillleurs j ene comprend pas quand vous me dites que -1 est racine du dénominateur.
car 4(-1+1)*(-1+2)*(-1+3) donne pas 0 .

Sinon tu peux écrire

par **wallen22** » 12 Sep 2009, 21:00

qu'est ce que je peux etre bete évidemment le dénominateur vaut 0 avec -1. excusez moi.

Merci!!! j'y suis enfin parvenu grace à vous!

je peux vous demander de l'aide pour un autre exo mais cette fois de spé qui concerne la récurrence et la divisibilité ?

encore merci!!!!

par **girdav** » 12 Sep 2009, 21:05

Oui, mais les modérateurs vont de demander d'ouvrir un nouveau topic.

par **wallen22** » 12 Sep 2009, 21:14

merci. mais je viens de me rendre compte que l'exo commencé n'est pas fini :

voilà la 2eme question :

a appartient à R*+
ON sait que pour tout n appartenant à N* (1+a)^n >ou égal 1+na

poser a =1/n pour établir pour tout n appartenant à N* (n+1=^n >ou égal 2n^n

voilà ce que j'ai commencé :

(1+a)^n > 1+na
(1+(1/n)) ^n > 1+(n*1/n)
((n+1)/n)) ^n > 2
[(n+1)^n / n^n ] >2
(n+1)^n > 2*n^n

c'est bien ça ?

par **wallen22** » 12 Sep 2009, 21:15

il y a une deuxième question mais je repasserai une fois que je l'aurais essayé, je vais poser un autre topic pour le nouvel exo de spé.

Récurrence terminale S

récurrence terminale S

Qui est en ligne