Question sur un signe.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
black2pac
- Membre Naturel
- Messages: 32
- Enregistré le: 13 Sep 2006, 20:37
-
 par black2pac » 12 Sep 2009, 14:31
par black2pac » 12 Sep 2009, 14:31
Bonjour à toi aussi !
Je suis en ECS et j'ai un problème qui peut paraitre stupide, mais pourtant je n'y arrive pas à savoir trouver le signe de :
ln((n+1)/n)-(1/(n+1))
Merci d'avance.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 12 Sep 2009, 15:12
par Nightmare » 12 Sep 2009, 15:12
Salut,
que fais-tu en cours actuellement?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 12 Sep 2009, 15:20
par Nightmare » 12 Sep 2009, 15:20
Une méthode simple :
=ln(n+1)-ln(n)=\Bigint_{n}^{n+1} \frac{dx}{x}\ge \(\inf_{x\in [n,n+1]} \frac{1}{x}\) \times \Bigint_{n}^{n+1} dx)
c'est à dire :
\ge \frac{1}{n+1}\times (n+1-n)=\frac{1}{n+1})
:happy3:
-
black2pac
- Membre Naturel
- Messages: 32
- Enregistré le: 13 Sep 2006, 20:37
-
 par black2pac » 12 Sep 2009, 15:28
par black2pac » 12 Sep 2009, 15:28
Aie, je suis très loin du résultat. Merci pour ton aide mais apparemment, je dois prouver le contraire. A savoir que le terme de gauche est inferieur au terme de droite car je dois démontrer que cette suite est décroissante.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 12 Sep 2009, 15:41
par Nightmare » 12 Sep 2009, 15:41
Le terme de gauche est bien supérieur à celui de droite, cela va donc être dur de prouver le contraire :lol3:
De quelle suite parles-tu sinon?
-
black2pac
- Membre Naturel
- Messages: 32
- Enregistré le: 13 Sep 2006, 20:37
-
 par black2pac » 12 Sep 2009, 15:47
par black2pac » 12 Sep 2009, 15:47
Je dois prouver que la suite Un = Grand sigma (de 1 à n) X (1/k) - ln(n) est décroissante.
J'ai donc calculé ce que faisait Un+1 - Un et cela m'a donné.
ln((n+1)/n)-(1/(n+1)
Donc d'après toi l'erreur est dans mon calcul précédent ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 12 Sep 2009, 15:50
par Nightmare » 12 Sep 2009, 15:50
U(n+1)-U(n) vaut plutôt 1/(n+1)-ln((n+1)/n) et non l'opposé :lol3:
-
black2pac
- Membre Naturel
- Messages: 32
- Enregistré le: 13 Sep 2006, 20:37
-
 par black2pac » 12 Sep 2009, 15:53
par black2pac » 12 Sep 2009, 15:53
Ouah, la pauvre erreur de signe de 6ème ! Je te remerci pour avoir souligné mon problème qui n'était pas mathématiques mais juste psychiatrique. ;)
-
black2pac
- Membre Naturel
- Messages: 32
- Enregistré le: 13 Sep 2006, 20:37
-
 par black2pac » 12 Sep 2009, 15:54
par black2pac » 12 Sep 2009, 15:54
Ah, j'ai oublié de dire que je ne compris rien à la première ligne de calcul que tu as fait, ces signes me sont encore inconnus.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 12 Sep 2009, 15:56
par Nightmare » 12 Sep 2009, 15:56
Tu n'as pas vu les intégrales en cours?
-
black2pac
- Membre Naturel
- Messages: 32
- Enregistré le: 13 Sep 2006, 20:37
-
 par black2pac » 12 Sep 2009, 16:03
par black2pac » 12 Sep 2009, 16:03
Si mais pas de cette façon enfin je ne vois pas du tout ce que veux dire ta ligne.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 12 Sep 2009, 16:16
par Nightmare » 12 Sep 2009, 16:16
Tu es d'accord avec les 2 premiers signes = ?
-
black2pac
- Membre Naturel
- Messages: 32
- Enregistré le: 13 Sep 2006, 20:37
-
 par black2pac » 12 Sep 2009, 16:27
par black2pac » 12 Sep 2009, 16:27
Je comprend les signes mais le fairt de mettre de l'integrale de dx/x
j'ai du mal à comprendre en fait ce que tu as a fait pour démontrer l'inégalité
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 12 Sep 2009, 16:52
par Nightmare » 12 Sep 2009, 16:52
Tu es d'accord que
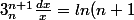-ln(n))
?
Ensuite, on sait que sur le segment [n,n+1], par décroissance de la fonction inverse,

En intégrant sur [n,n+1] on a donc :

Le membre de gauche vaut
-ln(n)=ln\(\frac{n+1}{n}\))
on l'a déjà dit, et le membre de droite vaut simplement
=\frac{1}{n+1})
On a bien l'inégalité souhaitée.
-
black2pac
- Membre Naturel
- Messages: 32
- Enregistré le: 13 Sep 2006, 20:37
-
 par black2pac » 12 Sep 2009, 18:15
par black2pac » 12 Sep 2009, 18:15
Parfait, je te remercie pour ton aide même si m'a compréhension fut laborieuse. Passe une bonne soirée.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités
