Terminale S, dénombrements

[Chantefleur]

Bonsoir tous !

J'ai un magnifique problème particulièrement vraisemblable à résoudre, qui fait suite au cours sur les dénombrements (entre autres, les notions de u-plets, arrangements, permutations, combinaisons, et quelques formules d'une complexité très relative).
Seulement moi, quand je vois les mots "singe" et "échelle", je cherche encore le rapport avec les 9h de cours qu'on a passées à compter les bulletins dans l'urne d'un bureau de vote...

Voici le problème en question, histoire que vous compreniez ma détresse :
"Un singe grimpe le long d'une échelle de 19 barreaux en progressant soit d'un barreau à la fois soit de deux. Il ne descend jamais. Combien de façons distinctes a-t-il d'arriver au sommet ?"

Je n'arrive pas à déterminer l'ensemble qui contient les éléments à dénombrer. 19, ça ne me semble pas idéal vu que c'est un nombre qui va varier en fonction du nombre de barreaux que le singe va décider de zapper...
Alors bien sûr je pourrais compter le nombre de possibilités lorsque le singe va toucher les 19 barreaux, puis lorsqu'il en touche 18, puis 17... non seulement ça me paraît long et fastidieux (je suis flemmarde à mes heures), mais à mon avis cette méthode plairait moyen à ma prof (je l'entends d'ici dire "ah là là, et s'il avait dû monter 2009 marches, hein, vous auriez fait comment ?...")
... du coup toutes les pistes de réflexion sont les bienvenues (quoique je soupçonne que ce soit précisément le type de problème où il suffit d'avoir l'étincelle de départ pour être capable de faire la suite en deux fois cinq minutes. Mais bon...)

Merci d'avance, donc.

PS : on ne tient pas compte du cas où le singe est trop fatigué pour monter jusqu'en haut. Dans mon lycée, les singes sont tous bien élevés, en pleine forme et très endurants. Non mais c'est vrai, quoi.

[fatal_error]

salut,

une premiere approche.
on va faire un peu de graphe, mais juste pour faire joli.
posons letat 0, cad que le singe a fini de monter.
on parle d'état n, lorsque le singe est au nieme barreau en partant de la fin.
On peut faire un graphe. (ok, en ascii parce que chui trop teubé pour gimp)
1-->0
Î \ Î
3-->2

Il faut voir que :
1 pointe vers 0
2 pointe vers 1 ou pointe vers 0 (le singe monte un barreau, ou deux)
3 pointe vers 2 ou vers 1 (le singe monte un barreau ou deux, donc passe du barreau 3 au barreau 2 ou bien directe au barreau 1)
De même 5 pointe vers 4 ou 3, etc...

Maintenant, on peut poser : soit u_n le nombre de possibilités d'arriver a letat 0 en étant a l'état n.
On remarque alors que

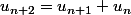
ex : en posant u_{n+2} pour letat 5, on somme les poss de letat 4 et celles de letat 3.
Il reste donc a résoudre cette jolie suite

[Chantefleur]

Merci beaucoup pour ta réponse.
J'ai un peu de mal avec le coup du graphe, je ne suis pas encore très initiée à cette "technique" (en fait pas du tout ^^) ; ceci dit, entre-temps j'ai cherché des cours sur les dénombrements, et la "chance" a voulu que cet exercice soit utilisé comme exemple.
En l'occurrence, la manière de le résoudre était de dire "si je suis à n barreaux du sol, si je monte d'un barreau je me ramène au cas où j'étais à n-1 barreaux du sol (par "cas" on entend nombre identique de barreaux restants identique donc nombre identique de possibilités). Et si je choisis de monter deux barreaux, je me ramène au cas n-2... d'où l'on retrouve la suite que tu m'as indiquée, qui porte si je me souviens bien des cours de l'an passé, le doux nom de Fibonacci.
Les deux méthodes sont basées je pense sur le même principe ? Celle que je viens d'écrire me parle davantage, sans doute parce qu'elle est plus "naïve" (mais malheureusement moins rigoureuse...)

Ceci dit, je suis bien embêtée, d'une part parce que jamais je n'aurais été capable de trouver ça toute seule, d'autre part parce que je ne vois toujours pas de rapport avec les dénombrements...
(à ce propos j'ai encore plein de gentils exercices avec des jeux de cartes, un mystérieux nombre de mains de huit cartes contenant tantôt trois coeurs et deux rois, tantôt un carré exactement... exprès rien que pour m'embrouiller. J'y réfléchis deux jours et après je poste si mon cerveau survit jusque-là.)

[fatal_error]

re, oui c'est la même méthode. pe que mon vocabulaire employé est pas assez explicite. De toute façon du moment que tu as saisi,..., ca roule.

Sinon, ben moi non plus, jy ai pensé parce que jai rencontré ce probleme récemment lol

[Chantefleur]

Bon, après consultation de ma prof, effectivement, elle ne veut pas que nous utilisions cette méthode. Ce sera du dénombrement et rien d'autre... elle va même jusqu'à prétendre que c'est simple ! Quelle honte.
*se prépare un thermos de café*

[Chantefleur]

Petit up ? Je cherche toujours, mais hélas ! ne trouve rien...