Suites, petit problème...
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
hps
- Membre Naturel
- Messages: 24
- Enregistré le: 10 Sep 2009, 18:09
-
 par hps » 10 Sep 2009, 18:10
par hps » 10 Sep 2009, 18:10
Bonsoir !
J'ai un petit exercice de suite dans lequel je suis bloqué et j'aurais besoin de votre aide

:
Alors l'énoncé est le suivant :
U0 = 1 et U1= 2
Un+2 = (3/2)Un+1 - (1/2)Un
Vn = Un+1 - Un
Donc j'ai montré que Vn était un suite géométrique de raison (1/2) et de premier terme V0 = 1 et j'ai exprimé Vn en fonction de n j'ia donc obtenu : Vn = (1/2)^n
Mais le problème maintenant c'est que l'on me demande d'exprimer Un en fonction de n, et je n'y arrive vraiment pas...
J'espère que quelqu'un a une piste à me proposer, je vous remercie d'avance.

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 10 Sep 2009, 19:23
par fatal_error » 10 Sep 2009, 19:23
salut,
On peut par exemple remarquer que :
)
la vie est une fête

-
hps
- Membre Naturel
- Messages: 24
- Enregistré le: 10 Sep 2009, 18:09
-
 par hps » 11 Sep 2009, 07:33
par hps » 11 Sep 2009, 07:33
Merci, j'ai essayé de voir un peu tout ça, et je retombe sur le même problème qu'avant :
 = U_(n+1) + \frac{1}{2}V_n)
Or une fois que j'ai cela, je me vois mal exprimer Un en fonction de n...
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 11 Sep 2009, 07:37
par girdav » 11 Sep 2009, 07:37
Bonjour.
On a
^n =u_{n-1} + \(\fr 12\)^{n-1}+\(\fr 12\)^n)
-
hps
- Membre Naturel
- Messages: 24
- Enregistré le: 10 Sep 2009, 18:09
-
 par hps » 11 Sep 2009, 07:52
par hps » 11 Sep 2009, 07:52
Je suis encore une fois tout à fait d'accord, cependant je suis incapable d'aller plus loin, je tourne sans cesse en rond...
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 11 Sep 2009, 08:21
par girdav » 11 Sep 2009, 08:21
On peut encore écrire
^{n-2}+\(\fr 12\)^{n-1}+\(\fr 12\)^n)
. Tu vois quelque chose apparaître?
-
hps
- Membre Naturel
- Messages: 24
- Enregistré le: 10 Sep 2009, 18:09
-
 par hps » 11 Sep 2009, 08:34
par hps » 11 Sep 2009, 08:34
Je vois, je vois. On va essayer d'écrire ça :
 = U_(n-k) + \sum_{i = 0}^k {V_(n-i)})
Aie j'ai peur de m'être trompé.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 11 Sep 2009, 08:41
par girdav » 11 Sep 2009, 08:41
hps a écrit:Je vois, je vois. On va essayer d'écrire ça :
 = U_(n-k) + \sum_{i = 0}^k {V_(n-i)})
Aie j'ai peur de m'être trompé.
Voilà, essaie de démontrer ça, puis prends
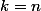
.
Sinon, c'est plus rapide de conjecturer que
^j)
et de le montrer par récurrence.
-
hps
- Membre Naturel
- Messages: 24
- Enregistré le: 10 Sep 2009, 18:09
-
 par hps » 11 Sep 2009, 09:04
par hps » 11 Sep 2009, 09:04
girdav a écrit:Voilà, essaie de démontrer ça, puis prends
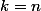
.
Sinon, c'est plus rapide de conjecturer que
^j)
et de le montrer par récurrence.
Ca ne serait pas plutôt
\(\fr 12\)^j)
avec (n-1) au lieu de n ?
Merci beaucoup de m'avoir autant assisté ^^ . Mais je vais encore faire mon ignorant mais j'ai du mal avec la récurrence là...
Pour le terme de rang initial 0 pas de problème mais après je me retrouve avec:
 = \frac{3}{2}U_(k+1) - \frac{1}{2}U_k)
 = U_(k+1) - \frac{1}{2}V_k)
Et je ne sais quoi faire de :
 + \Bigsum_{j=0}^_(n-1)\(\fr 12\)^j)
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 11 Sep 2009, 09:10
par girdav » 11 Sep 2009, 09:10
C'est

en haut de la somme si tu prends

comme membre de gauche.
Dans ce cas,
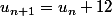^n\\<br /> = u_0 + \sum_{k=0}^{n-1}\(\fr 12 \)^k +\(\fr 12 \)^n)
et ça marche!
-
hps
- Membre Naturel
- Messages: 24
- Enregistré le: 10 Sep 2009, 18:09
-
 par hps » 11 Sep 2009, 09:38
par hps » 11 Sep 2009, 09:38
"Ca marche" = pas besoin de démontrer ?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 11 Sep 2009, 09:40
par girdav » 11 Sep 2009, 09:40
Je viens seulement de démontrer l'hérédité. A toi de faire l'initialisation, puis d'arranger l'écriture.
-
hps
- Membre Naturel
- Messages: 24
- Enregistré le: 10 Sep 2009, 18:09
-
 par hps » 11 Sep 2009, 09:44
par hps » 11 Sep 2009, 09:44
Ok.
Eh ben, en tout cas je te remercie girdav, d'avoir été patient et attentionné :we: , je n'ai plus qu'a essayé de rédiger tout ça au propre.
-
john03
- Messages: 1
- Enregistré le: 11 Sep 2009, 15:32
-
 par john03 » 11 Sep 2009, 15:44
par john03 » 11 Sep 2009, 15:44
Bonjour tout le monde,
J'ai un petit problème je n'arrive pas à justifier l'égalité suivante, :help:
Un industriel fabrique des boîtes de volume 1dm3 ( un dm cube ) ayant la forme d'un parallélépipède rectangle de hauteur y et dont la base est un carré de côté x supérieur à 0.
1. Justifier l'égalité y=1/2x²
2. En déduire que la somme des aires de toutes les faces de la boîte est 5(x)=2x²+4/x
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
