Raisonnemrnt par récurrence TS

[dragonfire]

Bonjours à tous et à toutes,
Je suis en terminal S et je fais des révisions de raisonnement par récurrence, pour être au niveau je fais des exos mais je bloque à un exo qui m'a l'air difficile :/ si une âme bienveillante pouvait m'aider :D :

Enoncé :
On s'intéresse ici à la somme Sn des cubes des n premiers entiers naturels impairs.

1) Calculer S1, S2, S3.
2) Démontrer par récurrence que, pour tout entier naturel n>1, on a Sn= 2n^4-n^2.
3)Quel est l'entier n pour lequel Sn= 41 328

Merci d'avance =)

[axwella]

supposont que (2) soit vrai,

je poserais l'equation: 41328 = 2n^4 - n^2

On a la forme: a^2 - b^2 =*... hum :)

ça pourrais être peer: Sophie Germain :)
- mais je suis jamais sure de moi -

[dragonfire]

je suis à la question 2 pas à la 3 si quelqu'un pouvait m'aider svp mais merci de ta réponse =)

[Ericovitchi]

par récurrence, tu vérifies qu'elle est vraie pour 1, tu supposes qu'elle est vraie pour 2n-1 et tu démontres qu'elle est vraie pour 2n+1
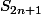
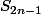
en calculant et en se servant de pour montrer que la formule est encore vraie pour 2n+1




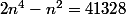
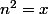
Pour le 2) il suffit de poser pour être devant un polynome du second degré.

[Cortos]

Salut

Ericovitchi, pourrais tu expliquer un peu plus ton raisonnement pour la question 2) stp ?

[Cortos]

Quand je verifie à la calculatrice je trouve que c'est faux.
Il me semble que l'erreur vient du fait qu'il y a une confusion entre le nombre impair suivant et le rang n mais je suis pas sûr
:hein: :hein: :hein: :hein: :hein: :hein: