Polynome

par **magnum** » 09 Sep 2009, 19:28

bonjour,

P(t)= x1/n! + [x2/(n+1)!]t + ...[xn/(2n-1)!]t^(n-1)

on pose f(t)= (t^n)P(t)

calculer f(1), f'(1)...dérivée (n-1)ième de f en 1.
En déduire les dérivée successives de P au point 1
Mq P est nul.

Pour la première question, j'ai dérivé à la main mais mon résultat contient tjrs une somme de xk sur des factoriels.

Merci !

par **Nightmare** » 09 Sep 2009, 19:30

Salut !

Sans faire de calculs j'ai deux idées en tête : Formule de Leibniz ou DL au point 1 !

par **magnum** » 09 Sep 2009, 19:33

La formule de Leibniz est vraiment affreuse ici, mais supposons que ça marche, comment tu déduirais la question 2 , si on est obligé de calculer les dérivées sucessives de P en 1 dès la 1 ère question ???

par **magnum** » 09 Sep 2009, 20:02

personne ?

par **abcd22** » 09 Sep 2009, 21:16

Bonsoir,
Qu'est-ce que c'est x1, ..., xn ?

par **fatal_error** » 09 Sep 2009, 22:01

salut

On peut aussi faire exprimer sous forme de serie, et faire 'rentrer'

, ou k est l'indice de sommation puis dériver terme a terme vu que n est fixé.

par **ToToR_2000** » 10 Sep 2009, 07:20

bonjour,

la formule de Leibniz n'est pas compliquée à utiliser ici.

Par contre, je partage ta perplexité sur la question: montrer que P est nul.
En effet, il n'a aucune raison de l'être, sauf si les

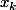
sont particuliers.

Polynome

polynome

Qui est en ligne