Titre non conforme - Attention

[iris17300]

Bonjour,
Je suis en Terminale S et je rencontre quelques difficultés sur mon premier Devoir Maison. Pouvez vous m'aider et/ou corriger mes réponses ?


soit f(x) = (x^2-3x+3)/(x-1)

1/ Étudier les variations de f.
J'ai essayé avec la dérivée mais je trouve croissant sur ]-inf;1[ ainsi que sur ]1;+inf[ alors qu'une fonction inverse est décroissante...

2/ Étudier les limites de f aux bornes de son domaine de définition.
Là aussi, autre incohérence, je trouve +inf quand x tend vers +inf et -inf quand x tend vers -inf...

3/ Dresser le tableau de variation.
J'ai mis que f(x) était décroissant dans les deux intervalles.

4/ Donner l'équation de la tangente à la courbe C au point d'abscisse 0.5.
y= f'(0.5)(x-0.5)+f(0.5)

5/ Calculer d(x)=f(x)-(x-2)
J'ai trouvé d(x)=1/(x-1)

a/ étudier le signe de d(x) en +inf et -inf. Que peut-on conclure pour C et D?
b/ calculer les limites de d(x) en +inf et -inf. Que peut-on conclure pour C et D?
J'ai trouvé que quand x tend vers +inf et -inf, d(x)=0

6/ Prouver que le point I(1;-1) est centre de symétrie de la courbe C.
Ça s'est bon, j'ai trouvé.

7/ Existe-t-il un point de la courbe C pour le quel la tangente à la courbe en ce point est parallèle à la droite D?
Je ne comprend pas cette question, je ne sais donc pas ce qu'il faut faire...

8/ Résoudre graphiquement l'inéquation f(x)>3
J'ai tracé la droite y=3 mais après je ne sais pas quoi faire d'autre.


Merci d'avance pour votre aide

[Ericovitchi]

non il y a des tas d'incohérences dans tes réponses. La fonction a un maximum et minimum et n'est pas toujours croissante.
tu dois avoir une erreur dans ta dérivé.
Tu devrais nous faire vérifier tes calculs de dérivée.

Pour 7/ il suffit de regarder s'il y a des x qui existe tels que f'(x)=2

Pour 8/ il faut regarder graphiquement s'il y a des points de la courbe qui sont au dessus de la droite y=3

Tu l'as dessiné ta courbe ?

[iris17300]

La dérivée est égale à (x^2-2x)/(x-1)^2

J'ai donc mis qu'elle était positive sur ]-inf;1[ et sur ]1;+inf[, ce qui revient à dire que la fonction est croissante. Et pourtant...

Pour la question 8, je n'étais pas sûre.

Merci

[Ericovitchi]

un bon moyen de ne pas se tromper dans les calculs c'est d'écrire ta fonction

la dérivée est alors immédiate :
et on voit bien qu'elle s'annule pour donc pour x=0 et x=2

Ta dérivé était juste mais pourquoi dis tu que (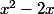 est toujours positif alors qu'il n'est positif qu'à l'extérieur des racines donc négative entre 0 et 2 ?

[iris17300]

Je ne comprend pas comment tu passes de f(x) à x-2+(1/x-1) ...?

[Ericovitchi]

D'abord en réduisant au même dénominateur on retombe bien sur ton expression du début.

Et puis dans ton problème tu as démontré que x-2 était asymptote oblique et que f(x) - (x-2) tendait vers zéro et était égal à 1/(x-1).

Mais sinon si on avait rien fait de tout ça, on aurait trouvé en cherchant à priori un forme d'équation ax+b+c/(x-1) et trouvé les coef en réduisant au même dénominateur et en égalant chaque coef de part et d'autre.

Ou enfin si on a appris il faut faire la division du polynôme par x-1 et on trouve x-2 comme quotient et 1 comme reste.