Theorème de sarkovskii

[nadiya13]

est ce que quelqu'1 connait le theorème de sarkovskii
merci a tous ceux qui prendront la peine de m'aider je les remercie d'avance

[abdo]

mais c est ds quel themes cet theorie
en algebre ou analyse...ect

[yos]

Théorème de Sarkozy : tout étranger capable de produire des théorèmes est le bienvenu.

[yos]

Bon je sors.

[memphisto]

Moi je sais, j'ai étudié sa démonstration en détails il y a environ 4 ans.
Mais j'ai pas les documents sur moi pour être suffisament précis.

En fait, pour l'expliquer, je vais prendre un exemple qui servira de modèle, simplifié certe, mais utile pour la compréhension.
Cet exemple est la fonction f, de [0,1] dans [0,1], qui à x associe , ou k est compris entre 0 et 4

[memphisto]

Le graphe de cette fonction rencontre la droite 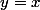en deux points:
0 et.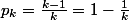

La fonction admet un maximum en , car sa dérivée s'annule (en changeant de signe) en ce point, et la valeur de f en ce point est:
(d'où le domaine de définition de k).

On étudie alors, pour chaque dans [0;1], la suite récurrente définie par .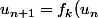
On voit immédiatement sur cet exemple que les points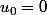 et 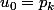sont des points fixes de , donc génèrent des suites constantes, égale à 0 pour la première, et égale à 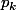pour la deuxième.
Mais qu'en est il des autres suites engendrées par les autres points de [0;1]?

Et bien c'est la dérivée en les points fixes de qui va déterminer le comportement des suites dans le voisinage de ces points fixes.
Si cette dérivée est en valeur absolue plus petite que 1, alors ce point fixe est attractif;
si cette dérivée est en valeur absolue plus grande que 1, alors ce point fixe est répulsif.

.
Donc , et .

On voit alors clairement que:

0 est attractif si 0 < k < 1, et répulsif si 1 < k <= 4.
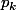est attractif si 1 < k < 3, et répulsif si 3 < k <=4
(et en particulier,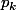 n'existe pas dans [0;1] pour 0 <= k < 1).

Chaque valeurs de k pour laquelle un point fixe donné est attractif définit un intervalle (qui dépend aussi de k) voisinage du point fixe considéré, qui est le "bassin d'attraction" de ce point fixe.
Tous les points de ce bassin génère une suite qui converge vers ce point fixe.

(faire un shéma de l'exemple, pour différentes valeurs de k, et étudier la pente de la derivée en les points fixes).

a suivre...

[memphisto]

On a donc:
Pour 0 <= k <= 1, le point 0 attire tout les points de [0,1].
Donc toutes les suites convergent vers 0, qui a donc pour bassin d'attraction [0,1].

Pour 1 < k <= 3, le point 0 devient répulsif, car la dérivée de en 0 est supérieure a 1, et le point 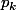attractif, car cette dérivée en 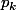est, en valeur absolue, plus petite que 1.
Donc hormis les points 0 et 1, qui engendrent tous deux une suite tendant vers 0, tous les autres points de ]0;1[ engendrent une suite convergente vers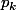 , qui a donc pour bassin d'attraction ]0;1[.

Pour 3 < k <= 4, les deux points fixes sont répulsifs, les suites ne convergent plus.
Mais leur comportent pour ces valeurs là de k ne sont pas totalement désordonnées. Il existe des suites cycliques, dont l'ordre est a déteminer, qui deviennent des cycles attractif: les suites engendrées ne convergent plus vers des points fixes (qui sont finalement des cycles de longeur 1), mais vers des cycles de longeur n arbitraire.

Ce que l'on vient de voir sur cet exmple, se généralise sans problèmes aux fonctions continues f, définies sur un intervalle I de R, et à valeurs dans cet intervalle I.

a suivre ...