Nombre de structures possibles...

par **achille** » 05 Sep 2009, 00:03

Salut tous,
J'ai une petite demande, sorte de question pas trop claire, mais c'est juste pour me guider avec d'éventuelles lectures, études ou domaines à aborder pour s'y faire, bon : a-t-on posé la question de déterminer le nombre de structures possibles sur un ensemble ? Par exemple : le nombre de structure loi de composition interne sur un ensemble fini, structure espaces vectoriels sur un ensemble, etc...
voilà merci :)

par **charlol** » 05 Sep 2009, 00:27

le nombre de structure loi de composition interne sur un ensemble fini :
si ton ensemble est de cardinal n, je dirais que le nombre de de structure de composition interne est le nombre de facon qu'on à d'associer un element a deux autres soit n^(2 parmi n) ^^
La question à deja du etre posée :++:
Une structure d'espace vectoriel, aucune idée et la réponse m'interesse.
D'ailleurs déja pour un groupe je me pose la question :id:

A bientôt

par **charlol** » 05 Sep 2009, 13:48

J'ai oublié que la loi de composition n'était pas forcément commutative pour l'ensemble quelconque la. Je pense que le nombre de loi de composition interne est donc le nombre de facon d'associer 2 éléments (eventuellement les mêmes) à deux éléments distincts, soit [(2 parmi n)+n]^(2 parmi n)
Corrigez moi si je me trompe :hum:
Voila c'était une remarque en passant :we:

par **mathelot** » 05 Sep 2009, 19:35

par **achille** » 05 Sep 2009, 19:52

mathelot a écrit:

je crois que c'est plutôt le cardinal des relations binaires sur E, une loi de composition interne (par exemple, je le mentionne puisque binaire...) n'est pas une relation binaire simple : il faut déterminer plutôt choisir un 'neutre', et lier spécifiquement deux éléments dans une relation de sorte à ce que leur produit fasse "e" (e le neutre)...

par **abcd22** » 05 Sep 2009, 20:24

charlol a écrit:D'ailleurs déja pour un groupe je me pose la question :id:

Il y a des chercheurs qui travaillent sur la classification des groupes finis, c'est exactement ça : pour chaque entier naturel n, ils cherchent toutes les structures de groupe possibles (à isomorphisme près) sur un ensemble à n éléments. J'avais vu un (gros) livre sur le sujet dans une bibliothèque une fois : c'était uniquement la liste des structures possibles jusqu'à je ne sais plus combien. Tout ça pour dire que c'est un problème qui est loin d'être évident ni résolu, et ça m'étonnerait qu'il existe une formule qui donne le nombre de structures de groupe sur un ensemble à n éléments en fonction de n, ou alors elle est complètement inutilisable.
Pour certaines valeurs de n c'est assez facile de trouver toutes les structures de groupe possibles, par exemple si n est premier il y en a une seule (et le groupe est nécessairement abélien), en utilisant les théorèmes de Sylow on peut trouver aussi la réponse pour certaines autres valeurs de n, après ça peut être compliqué...

par **abcd22** » 05 Sep 2009, 20:33

achille a écrit:je crois que c'est plutôt le cardinal des relations binaires sur E, une loi de composition interne (par exemple, je le mentionne puisque binaire...) n'est pas une relation binaire simple : il faut déterminer plutôt choisir un 'neutre', et lier spécifiquement deux éléments dans une relation de sorte à ce que leur produit fasse "e" (e le neutre)...

Là tu penses à une loi de groupe, qui est une loi de composition interne qui vérifie des propriétés particulières; une loi de composition interne sur un ensemble E c'est juste une application de ExE dans E qui ne vérifie pas nécessairement de propriétés particulières. Et une relation binaire sur E c'est une partie de ExE qui peut très bien être vide ou à l'autre extrême ExE tout entier, donc si E est de cardinal n, il y a

relations binaires possibles.

par **achille** » 05 Sep 2009, 23:47

abcd22 a écrit:Il y a des chercheurs qui travaillent sur la classification des groupes finis, c'est exactement ça : pour chaque entier naturel n, ils cherchent toutes les structures de groupe possibles (à isomorphisme près) sur un ensemble à n éléments. J'avais vu un (gros) livre sur le sujet dans une bibliothèque une fois : c'était uniquement la liste des structures possibles jusqu'à je ne sais plus combien. Tout ça pour dire que c'est un problème qui est loin d'être évident ni résolu, et ça m'étonnerait qu'il existe une formule qui donne le nombre de structures de groupe sur un ensemble à n éléments en fonction de n, ou alors elle est complètement inutilisable.
Pour certaines valeurs de n c'est assez facile de trouver toutes les structures de groupe possibles, par exemple si n est premier il y en a une seule (et le groupe est nécessairement abélien), en utilisant les théorèmes de Sylow on peut trouver aussi la réponse pour certaines autres valeurs de n, après ça peut être compliqué...

je me doutais que la question peut être délicate...te rappelles tu par hasard du nom du livre ou de son auteur ?
merci d'avance

par **abcd22** » 06 Sep 2009, 11:43

Pas du tout, enfin ça devait être un truc simple comme « Finite Groups » ou « Classification of Finite Groups », donc ça n'aide pas du tout. Si tu cherches sur google « "classification des groupes finis" » ou « "classification of finite groups" » (avec les guillemets droits (") dans la recherche) il y a des pages dessus qui ont des références.

par **achille** » 06 Sep 2009, 12:26

abcd22 a écrit:Pas du tout, enfin ça devait être un truc simple comme « Finite Groups » ou « Classification of Finite Groups », donc ça n'aide pas du tout. Si tu cherches sur google « "classification des groupes finis" » ou « "classification of finite groups" » (avec les guillemets droits (") dans la recherche) il y a des pages dessus qui ont des références.

bien alors merci

par **abcd22** » 06 Sep 2009, 20:23

J'ai oublié de dire dans mes messages précédents que pour les groupes abéliens finis il y a des théorèmes de décomposition en produits de groupes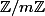

qui permettent de connaître tous les groupes abéliens de cardinal n à partir de n (même si pour les grands nombres ça ne doit pas être bien pratique à calculer); ce sont les groupes non abéliens qui posent problème. Tu as dû le découvrir toi-même si tu as cherché un peu sur internet mais je le précise quand même.

par **yos** » 07 Sep 2009, 16:12

abcd22 a écrit:Pour certaines valeurs de n c'est assez facile de trouver toutes les structures de groupe possibles, par exemple si n est premier il y en a une seule

n=3, E={a,b,c}. L'élément neutre peut être soit a, soit b, soit c, etc.
Tu réponds à une autre question on dirait.

par **Nightmare** » 07 Sep 2009, 16:19

Salut à tous :happy3:

Je profite de ce post pour poser une question à laquelle je n'ai jamais eu de réponse :

Etant donné un ensemble quelconque X, peut-on toujours munir X de bonne(s) loi(s) qui fasse(nt) de lui un groupe/corps ?

par **yos** » 07 Sep 2009, 16:27

Un ensemble fini peut toujours être muni d'une structure de groupe (cyclique par exemple). Idem pour dénombrable via une bijection avec Z. Idem pour continu via une bijection avec R, etc. (ça continue car l'ensemble des parties d'un ensemble est naturellement muni d'une structure de groupe).

Par contre un corps fini a pour cardinal une puissance d'un nombre premier, donc ...
Un ensemble infini, c'est bon via les corps Q,R,R(X), etc. A vérifier.

par **Nightmare** » 07 Sep 2009, 16:33

Salut yos ! Merci de ta réponse.

Il y a quelque chose qui me chiffonne, tu parles de transfert de structure mais on a besoin d'avoir des isomorphismes pour ça, on va peut être avoir une bijection avec les corps/groupes de base mais a-t-on toujours le transfert des lois?

par **yos** » 07 Sep 2009, 16:39

C'est un problème de chronologie.

Tu as un ensemble, par exemple dénombrable E. On a donc une bijection f de Z dans E. Pour x et y dans E, tu poses x * y = a + b, où a et b sont les antécédents de x et y par f.
On a donc transféré la structure de Z sur E. Et la bijection f devient un isomorphisme.

par **mathelot** » 07 Sep 2009, 16:42

tu poses x * y = f(a + b)= f(a) * f(b)

par **Nightmare** » 07 Sep 2009, 16:43

Effectivement, ça semble marcher.

par **abcd22** » 07 Sep 2009, 16:46

yos a écrit:n=3, E={a,b,c}. L'élément neutre peut être soit a, soit b, soit c, etc.
Tu réponds à une autre question on dirait.

Je réponds à isomorphisme près, sinon on n'a pas fini...

Edit : C'était d'ailleurs précisé dans le message que tu cites, même si je ne l'ai pas répété à chaque fois.

par **yos** » 07 Sep 2009, 16:52

abcd22 a écrit:Je réponds à isomorphisme près, sinon on n'a pas fini...

Et si on te demande le nombre de l.c.i. sur {a,b,c} ? Car c'est bien ainsi que la question est posée au premier message.

il y a 19683 lci sur {a,b,c}, dont 3 sont des lois de groupe (à vérifier).

Nombre de structures possibles...

nombre de structures possibles...

Qui est en ligne