Bonjour à tous, je viens de commencer mon cours d'algèbre, et je bloque sur un problème. Il s'agit d'une démonstration, mais on a à peine eu le temps d'en faire une avec le professeur en classe.
Le problème va comme suit:
Soit v un vecteur non nul. Quelle est la valeur du scalaire k pour laquelle v/k est un vecteur unitaire (de longueur 1) ? ( note: v/k = (1/k)v )
Je dois démontrer cela à l'aide de théorèmes avec une démarche complète, mais je ne sais même pas ou commencer!!
Question d'algebre
9 messages
- Page 1 sur 1
geegee a écrit:Bonjour,
On veut que ||v/k|| = 1
Donc que ||v|| = k car on peut s'ortir k de la norme car c'est un réel.
Donc k = ||v|| ou -...
Bonjour, comment tu fais pour passer de ||v/k|| = 1 à ||v|| = k ? Je comprends le raisonnement (que pour qu'un nombre divisé par quelque chose donne 1, il doit automatiquement être divisé par lui-même), mais existe-til un théorème expliquant cela? J'essaie de comprendre comment faire des démonstrations en justifiant toutes les étapes, et c'est là que je bloque.
De plus, comment tu sais que k = || v || ou k = - || v || ? Est-ce qu'on peut dire que - || v || = || v || ?? Comment est-ce possible?
Oh, et je m'excuse si mon manque de connaissances vous découragent, mais comme je l'ai mentionné, le professeur n'a pratiquement rien montré, alors je veux bien essayer d'apprendre par moi-même mais c'est difficile. C'est pour ca que je me dis que quelque chose va bien "cliquer" si quelqu'un m'explique cela. (J'ai vraiment de la facilité à comprendre habituellement)
désolé du retard.
En faite le raisonnement c'est qu'un vecteur unitaire c'est de norme 1 donc on doit avoir un nombre qui se divise par lui meme comme mathieu444 l'as dis ou par son opposé car ||v/-||v|||| =||-1||
car Propriété
La norme du produit par un nombre est le produit de la norme par la valeur absolue de ce nombre :

Donc
Or
car Propriété
Pour tous a,b appartenant à R , |ab| = |a|x|b|
Donc implique
implique 
Or |-k| = |k|
Ou Propriété:
En particulier, tout vecteur a la même norme que son opposé :
Donc k =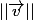 ou -
ou - 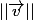
En faite le raisonnement c'est qu'un vecteur unitaire c'est de norme 1 donc on doit avoir un nombre qui se divise par lui meme comme mathieu444 l'as dis ou par son opposé car ||v/-||v|||| =||-1||
car Propriété
La norme du produit par un nombre est le produit de la norme par la valeur absolue de ce nombre :
Donc
Or
car Propriété
Pour tous a,b appartenant à R , |ab| = |a|x|b|
Donc
Or |-k| = |k|
Ou Propriété:
En particulier, tout vecteur a la même norme que son opposé :
Donc k =
J'ai retravaillé un peu le problème, est-ce que ma solution semble correcte??
v / k = 1 (car un nombre divisé par lui-même donne 1, par propriété)
|| v || / |k|| = 1 (par définition du produit d'un vecteur par un scalaire, || kv || = |k| || v ||. Donc, || v/k || = || v || / |k|)
|| v || = 1 |k| (multiplication par |k| de l'équation)
v = + ou - k, donc k = + ou - v (k peut être positif ou négatif, par définition de la fonction valeur absolue)
v / k = 1 (car un nombre divisé par lui-même donne 1, par propriété)
|| v || / |k|| = 1 (par définition du produit d'un vecteur par un scalaire, || kv || = |k| || v ||. Donc, || v/k || = || v || / |k|)
|| v || = 1 |k| (multiplication par |k| de l'équation)
v = + ou - k, donc k = + ou - v (k peut être positif ou négatif, par définition de la fonction valeur absolue)
mathieu444 a écrit:J'ai retravaillé un peu le problème, est-ce que ma solution semble correcte??
v / k = 1 (car un nombre divisé par lui-même donne 1, par propriété)
|| v || / |k| = 1 (par définition du produit d'un vecteur par un scalaire, || kv || = |k| || v ||. Donc, || v/k || = || v || / |k|)
|| v || = 1 |k| (multiplication par |k| de l'équation)
v = + ou - k, donc k = + ou - v (k peut être positif ou négatif, par définition de la fonction valeur absolue)
Oui c'est cela
||v / k|| = 1 (car un nombre divisé par lui-même donne 1, par propriété et que l'on souhaite un vecteur unité)
|| v || / |k| = 1 (par définition du produit d'un vecteur par un scalaire, || kv || = |k| || v ||. Donc, || v/k || = || v || / |k|)
|| v || = 1 |k| (multiplication par |k| de l'équation)
(v = + ou - k) || v || = 1 |k|, donc k = + ou - ||v|| (k peut être positif ou négatif, par définition de la fonction valeur absolue |-k| =|k| oui k étant un scalaire il peut prendre soit + ou - ||v|| car ||v / k|| = ||v / -k|| = 1 pour k = + ou - ||v|| )
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 84 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
