Bonjour à tous,
Je cherche de la biblio sur les suites récurrentes à valeurs vectorielles. J'ai un problème de type u(n)=Au(n-1)+Bu(n-2) avec u0 et u1 connus ; u(k) vecteur ; A et B matrices. Je ne sais pas du tout comment l'attaquer.
Merci d'avance.
Cordialement,
Yohan.
Suites récurrentes à valeurs vectorielles
5 messages
- Page 1 sur 1
idée :
essaye d'exprimer u2 en fonction de u1 et u0 puis u3 en fonction de u1 et u0 ..... avec un peu de chance tu peu voir ce qui va se passer pour uk.
u2 = Au1 + Bu0
u3 = (AA + B)u1 + ABu0
..................................
une fois la formule trouvé, après essaye de la demonter par reccurence.
conseil : fait attention a l'ordre des matrices lors des multiplication i.e. A*B est diff B*A
bon courage
essaye d'exprimer u2 en fonction de u1 et u0 puis u3 en fonction de u1 et u0 ..... avec un peu de chance tu peu voir ce qui va se passer pour uk.
u2 = Au1 + Bu0
u3 = (AA + B)u1 + ABu0
..................................
une fois la formule trouvé, après essaye de la demonter par reccurence.
conseil : fait attention a l'ordre des matrices lors des multiplication i.e. A*B est diff B*A
bon courage
Salut,
Tout d'abord, merci pour ta réponse Zerroudi. Je vais ajouter quelques précisions et poser mon problème un peu plus proprement.
La première chose, c'est qu'il s'agit d'un problème qui n'admet pas forcément une solution simple. Je suis tombé dessus en déroulant des équations de changement d'échelles/calculs des moments d'ordre n associés au transport de masse dans un milieu poreux diphasique.
Ensuite, pour la partie technique, j'ai essayé d'écrire les éléments de ma suite en fonction de u0 et u1 et je ne vois rien de simple apparaitre.
Mon problème complet est le suivant, si vous voulez vous amuser avec moi (sinon de la biblio me serait très utile et certainement suffisante) :
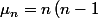A^{-1}D\mu_{n-2}+nA^{-1}V\mu_{n-1} \\<br />\mu_{1}=A^{-1}V\mu_{0})
A, D et V sont des matrices 2x2 inversibles à coeffs complexes (à la base je travaille avec une équa diff en temps que j'ai passée dans l'espace de Laplace). J'aimerais exprimer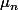 en fonction de
en fonction de  .
.
Cordialement,
Yohan.
Tout d'abord, merci pour ta réponse Zerroudi. Je vais ajouter quelques précisions et poser mon problème un peu plus proprement.
La première chose, c'est qu'il s'agit d'un problème qui n'admet pas forcément une solution simple. Je suis tombé dessus en déroulant des équations de changement d'échelles/calculs des moments d'ordre n associés au transport de masse dans un milieu poreux diphasique.
Ensuite, pour la partie technique, j'ai essayé d'écrire les éléments de ma suite en fonction de u0 et u1 et je ne vois rien de simple apparaitre.
Mon problème complet est le suivant, si vous voulez vous amuser avec moi (sinon de la biblio me serait très utile et certainement suffisante) :
A, D et V sont des matrices 2x2 inversibles à coeffs complexes (à la base je travaille avec une équa diff en temps que j'ai passée dans l'espace de Laplace). J'aimerais exprimer
Cordialement,
Yohan.
busard_des_roseaux a écrit:bonjour,
l'ensemble de ces suites est un e.v (sur R ou son complexifié C)
le terme général u_n dépend linéairement des deux premiers vecteurs
u_0 et u_1
en posantet une grande matrice
ça devient
d'où une suite géométrique ?
Bonjour et merci de ta réponse Busard,
Je connaissais cette technique pour des scalaires mais je ne savais pas que tu pouvais faire la même chose en écrivant une matrice par blocs... Je vais essayer de vérifier si ça marche.
Cordialement,
Yohan.
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
