Complexes
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Ryuk
- Membre Naturel
- Messages: 13
- Enregistré le: 28 Aoû 2009, 07:46
-
 par Ryuk » 28 Aoû 2009, 08:12
par Ryuk » 28 Aoû 2009, 08:12
Bonjour!! Tu es nouveau sur le forum: je t'invite à aller d'urgence lire le réglement!
J'ai un petit problème avec (x + iy)² = 1+i
Je n'arrive pas a trouver x et y , je m'en remet à vous
 par Dominique Lefebvre » 28 Aoû 2009, 08:23
par Dominique Lefebvre » 28 Aoû 2009, 08:23
Bonjour,
Développe le terme de gauche et procède par identification
-
Ryuk
- Membre Naturel
- Messages: 13
- Enregistré le: 28 Aoû 2009, 07:46
-
 par Ryuk » 28 Aoû 2009, 08:33
par Ryuk » 28 Aoû 2009, 08:33
ce qui nous donne
x²-y² =1
2xy = 1 <=> x = 1 /(2y)
1/(4y²) - y² = 1
mais je trouve que ça donne rien
-
echevaux
- Membre Relatif
- Messages: 276
- Enregistré le: 06 Juin 2006, 16:08
-
 par echevaux » 28 Aoû 2009, 08:53
par echevaux » 28 Aoû 2009, 08:53
Bonjour
Essaie d'utiliser module et argument :
ceux de 1+i sont simples à calculer.
tu peux en déduire ceux de x+iy ...
-
Black Jack
 par Black Jack » 28 Aoû 2009, 09:02
par Black Jack » 28 Aoû 2009, 09:02
Ryuk a écrit:ce qui nous donne
x²-y² =1
2xy = 1 x = 1 /(2y)
1/(4y²) - y² = 1
mais je trouve que ça donne rien
- mutiplie les 2 membres par 4y² ...
- Et puis pose y² = Y ...
*******
Ou bien alors utilise la méthode suggérée dans le message précédent
:zen:
-
Ryuk
- Membre Naturel
- Messages: 13
- Enregistré le: 28 Aoû 2009, 07:46
-
 par Ryuk » 28 Aoû 2009, 09:14
par Ryuk » 28 Aoû 2009, 09:14
ça donne ( x + iy)² =
)
mais après je vois pas comment développer plus :triste:
je vais essayer ta proposition
-
egan
- Membre Rationnel
- Messages: 668
- Enregistré le: 03 Juil 2009, 15:32
-
 par egan » 28 Aoû 2009, 09:19
par egan » 28 Aoû 2009, 09:19
EDIT modération : c'est la dernière fois que je te dis qu'on ne donne pas la solution!!
J'espère que ya pas d'erreur, lol. :ptdr:
-
Ryuk
- Membre Naturel
- Messages: 13
- Enregistré le: 28 Aoû 2009, 07:46
-
 par Ryuk » 28 Aoû 2009, 09:25
par Ryuk » 28 Aoû 2009, 09:25
Avec l'equation de second degré je trouve
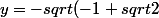/2} //<br /> y = sqrt{(-1+sqrt{2})/2}//<br /> y = -sqrt{(-1-sqrt{2})/2} //<br /> y = sqrt{(-1-sqrt{2})/2})
je ne pense pas que ce soit ça
les 4 solutions que je trouve ne marchent pas
-
Miche
- Messages: 1
- Enregistré le: 28 Aoû 2009, 10:38
-
 par Miche » 28 Aoû 2009, 10:40
par Miche » 28 Aoû 2009, 10:40
c'est vrai que ça ne marche pas car ça donne sinus > 1 et pour l'autres une racine négative , je ne sais pas
-
echevaux
- Membre Relatif
- Messages: 276
- Enregistré le: 06 Juin 2006, 16:08
-
 par echevaux » 28 Aoû 2009, 13:33
par echevaux » 28 Aoû 2009, 13:33
Ryuk a écrit:Avec l'equation de second degré je trouve

je ne pense pas que ce soit ça
les 4 solutions que je trouve ne marchent pas
J'en vois pourtant une qui "marche" très bien.
-
mathelot
 par mathelot » 28 Aoû 2009, 15:42
par mathelot » 28 Aoû 2009, 15:42
Ryuk a écrit:Bonjour!! Tu es nouveau sur le forum: je t'invite à aller d'urgence lire le réglement!
J'ai un petit problème avec (x + iy)² = 1+i
Je n'arrive pas a trouver x et y , je m'en remet à vous
le truc classique, c'est de rajouter une égalité, obtenue avec les modules
des deux membres:
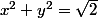
avec cette remarque, on obtient un système 2x2 d'inconnues

et
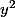
et l'on trie les 4 solutions obtenues (deux de trop!)
en regardant le signe du produit xy>0

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 28 Aoû 2009, 17:06
par Ericovitchi » 28 Aoû 2009, 17:06
je ne comprend pas bien pourquoi vous ne suiviez pas la proposition faite au dessus de faire par le module et l'argument. c'est instantané ou presque.
^2=1+i= \sqrt{2}e^{i \frac {\pi}{4}+k2\pi})
donc
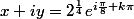
et puis c'est tout, non ?
-
mathelot
 par mathelot » 29 Aoû 2009, 09:19
par mathelot » 29 Aoû 2009, 09:19
Ericovitchi a écrit:je ne comprend pas bien pourquoi vous ne suiviez pas la proposition faite au dessus de faire par le module et l'argument. c'est instantané ou presque.
^2=1+i= \sqrt{2}e^{i \frac {i\pi}{4}+k2\pi})
donc
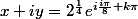
et puis c'est tout, non ?
c'est l'éternelle question:
préfère t on une solution écrite avec
)
ou sous la forme

?
pour obtenir des valeurs approchées des solutions, sans calculatrice, de toute façon, il y a du taf , méthode Cordic pour la solution trigo, méthode de Newton pour la solution cartésienne.

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 29 Aoû 2009, 10:41
par Ericovitchi » 29 Aoû 2009, 10:41
si on veut Cos(Pi/8), sachant que
 = \frac{\sqrt{2}}{2})
on peut aussi le calculer facilement avec la formule
 = \sqrt{\frac {1+cos(2\theta)}{2}})
= \frac{\sqrt{2+\sqrt{2}}}{2})
et
= \frac{\sqrt{2-\sqrt{2}}}{2})
mais il ne me viendrait pas à l'idée de résoudre un problème de façon compliqué juste pour avoir au final la valeur de cos(pi/8).
-
mathelot
 par mathelot » 31 Aoû 2009, 13:02
par mathelot » 31 Aoû 2009, 13:02
Ryuk a écrit:Bonjour!! Tu es nouveau sur le forum: je t'invite à aller d'urgence lire le réglement!
J'ai un petit problème avec (x + iy)² = 1+i
Je n'arrive pas a trouver x et y , je m'en remet à vous
allez vite fait,
en cartésien, on rajoute une équation:
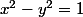
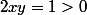
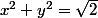
(avec les modules
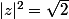
)
le système donne:
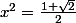
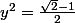
x et y sont de même signe (2 positifs ou deux négatifs)
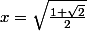
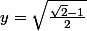
en résolvant en trigo
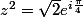
on obtient:
=\frac{\sqrt{1+\sqrt{2}}}{2} > 0)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 81 invités
donc
et puis c'est tout, non ?

