Bonsoir,
voila l'exercice est le suivant : montrer que
x^(2n)-1=(x²-1) * Prod(x²-2*x*cos(kPi/n)+1,k=1....n-1)
j'espere que c'est assez comprehensible...
alors voila c'est assez confus....
je resoud l'equation x^(2n)=1 en posant x=r*exp(ia)
et donc jaurais dans ce cas ci r=1 et a=k*Pi/n avec k variant de 0 à 2n-1
et donc le resultat est le suivant
x^(2n)-1= 1*Prod(X-exp(i*k*Pi/n), k=0...2n-1)
du coup il y a un probleme dans les indices....et apres avoir extrait juste la partie reele en cos , ca ne donne pas le resultat voulu....
vous me suivez?
j'espere que vous pouvez m'eclairer sur mon eventuelle erreur...
Racines complexes
9 messages
- Page 1 sur 1
au risque de paraitre enervante ( et idiote... :hein: )il y a deja un 2 au numerateur pour la racine n-ieme donc ca se simplifie pour la racine 2n-ieme et don il ne reste plus qu'un n au denominateur...
et je suis d'accord pour le develloppement a faire mais je n'ai pas ce produit (X-z)(X-zbar) dans factorisation premiere...
desolée mais la je suis assez embrouillé
et je suis d'accord pour le develloppement a faire mais je n'ai pas ce produit (X-z)(X-zbar) dans factorisation premiere...
desolée mais la je suis assez embrouillé
les réponses sont écrites en blanc. ne les regarde pas tout
voilà quelques questions destinées à aider:
i) combien le polynôme a-t-il de racines ?
a-t-il de racines ?
retrouve le nom du théorème très célébre qui va avec: D'A..G....
le polynôme a 2n racines, comptées avec leur ordre de multiplicité
içi, les racines sont simples. c'est le théorème de d'Alembert-Gauss
ii)combien a t il de racines réelles ?
=((x^n)^2-1)=(x^n-1)(x^n+1))
on voit que si n est pair, n'a pas de racines réelles
n'a pas de racines réelles
car il reste supérieur ou égal à 1 si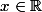
le polynôme a exactement 2 racines réelles, 1 et -1
on le voit en considérant l'argument (forme trigo) des racines.
iii)
qu'est ce qu'ont de particulier les racines non réelles d'un polynôme
à coefficients réels ?
on les groupe par paires, une racine et sa conjuguée
iv)
que vaut le module des racines (ce sont des nombres complexes)
du polynôme
leur module vaut 1
v) si |z|=1, comment s'écrivent z puis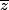 ?
?
developpe alors(x-\bar{z})) dans ce cas |z|=1,
dans ce cas |z|=1,
en s'aidant de la forme trigo de z.
z=e^{i \theta} et zbar=e^{ - i \theta}
(x-z)(x-zbar)=x^2 - 2 cos(\theta)x +1)
i) combien le polynôme
retrouve le nom du théorème très célébre qui va avec: D'A..G....
le polynôme a 2n racines, comptées avec leur ordre de multiplicité
içi, les racines sont simples. c'est le théorème de d'Alembert-Gauss
ii)combien a t il de racines réelles ?
on voit que si n est pair,
car il reste supérieur ou égal à 1 si
le polynôme a exactement 2 racines réelles, 1 et -1
on le voit en considérant l'argument (forme trigo) des racines.
iii)
qu'est ce qu'ont de particulier les racines non réelles d'un polynôme
à coefficients réels ?
on les groupe par paires, une racine et sa conjuguée
iv)
que vaut le module des racines (ce sont des nombres complexes)
du polynôme
leur module vaut 1
v) si |z|=1, comment s'écrivent z puis
developpe alors
en s'aidant de la forme trigo de z.
z=e^{i \theta} et zbar=e^{ - i \theta}
(x-z)(x-zbar)=x^2 - 2 cos(\theta)x +1)
lolita2 a écrit:au risque de paraitre enervante ( et idiote... :hein: )il y a deja un 2 au numerateur pour la racine n-ieme donc ca se simplifie pour la racine 2n-ieme et don il ne reste plus qu'un n au denominateur...
et je suis d'accord pour le develloppement a faire mais je n'ai pas ce produit (X-z)(X-zbar) dans factorisation premiere...
desolée mais la je suis assez embrouillé
Je suis d'accord (on retrouve d'ailleurs le
la suite est un peu compliquée, pourriez vous m'aider a comprendre?
on nous demande den deduire la valeur de integrale de 0 à Pi de
ln(a²-2acost+1)dt avec a appartent a Rprivé de -1 et 1 ....
j'ai donc pris le ln de l'egalité precedente et jobtiens la somme de ln(a²...) comment passer à l'integral?
Merci d'avance
on nous demande den deduire la valeur de integrale de 0 à Pi de
ln(a²-2acost+1)dt avec a appartent a Rprivé de -1 et 1 ....
j'ai donc pris le ln de l'egalité precedente et jobtiens la somme de ln(a²...) comment passer à l'integral?
Merci d'avance
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
