équations aux dérivées partielles

par **Paradox** » 24 Aoû 2009, 10:42

Bonjour,
je suis perdu dans la résolution des équations aux dérivées partielles du second ordre...

Je cherche à déterminer les dérivées partielles d'ordre 2, mais je n'y arrive pas.
La fonction est quelconque, on a f(x,y) et on utilise g(u,v) comme changement de variable.

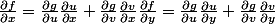
J'aimerais trouver

, mais je ne sais pas comment faire...

Merci d'avance :briques:

par **mathelot** » 24 Aoû 2009, 11:27

içi .......................................

par **Paradox** » 24 Aoû 2009, 11:52

ben merci mais je ne vois pas trop le rapport avec les composées et les sinus/cosinus ..................................... ce qui m'intéresse c'est le cas général, la fonction n'étant pas forcément trigonométrique :|

par **flo22** » 24 Aoû 2009, 13:11

Si tu veux mathelot je vais essayé de lui expliquer je pense avoir compris maintenant ^^

à partir de ça, tu dérives

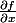
en utilisant à la fois la formule classique de dérivée d'un produit et de composée de deux fonctions, exactement celle que tu as utilisée.

par **mathelot** » 24 Aoû 2009, 13:24

flo22 a écrit:Si tu veux mathelot je vais essayé de lui expliquer je pense avoir compris maintenant ^^

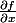
à partir de ça, tu dérives en utilisant à la fois la formule classique de dérivée d'un produit et de composée de deux fonctions, exactement celle que tu as utilisée.

géniaaal. n'hésite pas à lui envoyer les documents (pdf) de calcul différentiel s'il
le souhaite. :we:

très cordialement.

par **Paradox** » 24 Aoû 2009, 13:53

ça y est j'ai pigé :we: mes souvenirs étaient un peu brumeux, et en fait ça sert à rien d'avoir une formule toute faite. suffit de réinjecter la dérivée dans la formule :D

merci à tous

par **flo22** » 24 Aoû 2009, 13:56

oui tout à fait, moi pareil je m'étais créer des difficultés pour rien. A+

équations aux dérivées partielles

équations aux dérivées partielles

Qui est en ligne