Exercice basique, je dois être folle, je n'y arrive pas^^

[nor]

Bonjour!! Je te prie d'aller consulter le réglement d'urgence!

On considére la fonction f de R vers R définie par f(x)=ax²+bx+c , a,b et c étant trois constantes réelles, et on désigne par P la parabole représentative de f dans un repère du plan. Calculer a, b et c de manière à ce que P passe par les points: A (1;0) B(2;3/2) et C(3;5) Calculer ensuite les coordonnées du sommet de P.


voilà donc remplace:

0= a+b+c
3/2= 4a+2b+c
5= 9a+3b+c

Ce qui me donne un systeme:

a= -b-c
3/2=4(-b-c)+2b+c
5=9a+3x+c

Voilà et après, si je continue, j'arrive toujours pas à trouver un des trois (a ou b ou c) pour continuer.

ps: l'autre question je vois comment la faire, mais il me faut a, b c.

Comment faire ?!

[Edward]

Dans ta deuxième équation tu n'a que b et c comme inconnues, tu peut donc exprimer l'une en fonction de l'autre, et comme a s'exprime en fonction de b et c tu arrivera à résoudre ton système.

Sinon essaye de modifier ta 3e ligne comme avec la 2e, une petite opération devrait alors sauter aux yeux ^^

[nor]

Non franchement je dois fais un blocage quand je continue le calcul de la deuxiéme ligne, je trouve b=-3/4-3/2c et après je sais plus quoi faire.

[Edward]

La par exemple t'a b en fonction de c. Si dans ta 3e ligne tu remplace a par -b-c et après b par son expression (en fonction de c), tu n'auras plus que c comme inconnue, et tu pourra trouver sa valeur.

[nor]

ouai j'ai fait ça, je trouve 38/212=c bon je suis extremment fatiguée, j'ai pas dormi de la nuit. C'est peut être à cause de ça.

[Edward]

Oula je trouve 1/2 ^^ je te poste le détail :


On remplace dans la 3e ligne qui est :

[nor]

ha merci, bon derniere question, euh la
3éme ligne c'est 5= 9a+3b+c et pas 5=-6b-c (comment t'as fait)

[Edward]

Tout comme tu avis fait pour la 2e ligne, remplace a par -b-c. Il te reste alors b et c, et comme tu connais c ...

[nor]

VOilà donc je trouve a=1 b=-9/6 c=1/2

[Edward]

Voilà c'est ça. Tu peux même simplifier b en -3/2

[nor]

Merci beaucoup d'avoir autant de patience vraiment :)

j'ai juste un dernier exos qui me tracasse, qui es dans la même lignée.

On considére une fonction f définie sur R par: f(x) ax^3+bx^2+cx+. Dans un repère du plan, la représentation graphique C de F passe par les points:
A(0;1), B(-2;5) et E(-1;3), et les tangentes à C en A et B sont horizontales. Determiner les réels a, b, c et d. En déduire une équation de la tangente en E à la courbe C.

Voilà donc je me doute qu'il faut faire comme l'autre, cependant nous avons 4 inconnu et seulement 3 points. C'est là que va apparaitre l'utilisation des tangentes. Mais je ne vois pas comment faire.

[Edward]

Ta fonction est polynomiale, elle est donc dérivable, de plus la dérivée de f en 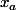(par exemple) est égal au coefficient directeur de la tangente à ta courbe représentative au point A. Donc si tes tangentes sont horizontales, ça veut dire que ce nombre dérivé est nul. Ca devrait de rajouter quelques équations ^^.

[nor]

Bon j'abandonne, je suis trop fatiguée, j'ai vraiment pas dormi de la nuit.
En tout cas merci pour tout, c'est vraiment gentil de voir que des gens sont là pour aider les autres :)

[Edward]

Mais c'est normal. Bon repos à toi ^^