Tan(x)=x, somme d'une série.

[Nightmare]

Bonsoir à tous :happy3:

Voici un exercice que j'ai trouvé sympathique, je vous le soumets car je recherche une preuve plus élémentaire que la mienne (qui passe par la théorie des résidus).

Il s'agit de montrer que si est la suite croissante des zéros réels positifs de l'équation tan(x)=x alors .

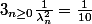
Bon courage.

:happy3:

[Doraki]

Hmm on peut dire que

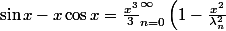et calculer la dérivée 5ème de ces choses ?
Mais j'imagine que l'analyse complexe nécessaire pour faire tout ça n'est pas plus élémentaire que la théorie des résidus.

[Nightmare]

Salut doraki :happy3:

Non effectivement ça revient un peu au même niveau difficulté :lol3: Je suis étonné qu'un énoncé si simple n'ait pas une preuve d'un niveau moins élevé...

[Doraki]

C'est pas parceque l'énoncé d'un théorème est simple qu'il en existe une preuve simple.
(par exemple, théorème de fermat...)

[yos]

Bonjour.
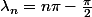
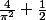
Si tu écris (ce qui est presque vrai), tu trouves que ta série vaut . C'est pas si mal...
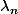
Plus sérieusement, un d.a. de est pas trop dur.

[Pythales]

Voici une démonstration inspirée d'Euler :
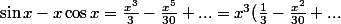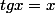
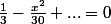
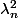
Si on excepte la valeur l'équation s'écrit et les sont solutions de
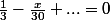
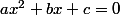
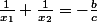
Or, si il est facile de voir que , ce qui peut se généraliser pour une équation de degré n : la somme des inverses des racines est égale à
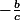
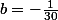
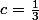
Ici et soit

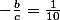
[yos]

ce qui peut se généraliser pour une équation de degré n :

Avec n infini... La justification demande pas mal d'analyse complexe je crois (c'est peut-être Hadamard qui a justifié ça rigoureusement).
En tout cas c'est convaincant.

[Pythales]

Bonjour
Je remets cette question sur le tapis car je me trouve face à un paradoxe.
Soit l'équation qui peut s'écrire
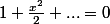
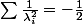
L'application de la méthode précédente conduit à , ce qui est paradoxal, les racines étant visiblement réelles.
Quelqu'un aurait-il une explication ?

[skilveg]

Bonjour,

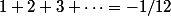
Peut-être que les inverses de ces solutions ne sont pas de carré sommable... C'est comme d'écrire à la Euler "" ou "".

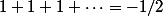
Pour la solution de cet exercice, j'ai vu ça dans une feuille de TD (c'est d'ailleurs peut-être la même source que Nightmare ^^), il faut intégrer très astucieusement une fonction introuvable (je trouve) sur un contour "convenable".

[Edit: le coup des inverses pas carré-sommables n'est pas très convaincant, puisque les solutions réelles sont visiblement coincées entre deux progressions arithmétiques... Tu es sûr que toutes les solutions sont bien réelles?]

[Pythales]

Merci.
Par curiosité, pourrais-tu me donner cette fonction "introuvable" et le contour ?
Cela dit, j'ai moi aussi pensé qu'en plus des solutions réelles, il pouvait exister des solutions complexes.
Mais comment le prouver ?

[skilveg]

C'est .

[Pythales]

Merci. Et je suppose que le contour est un cercle de rayon infini.

[skilveg]

Oui il me semble, ou plutôt un rectangle, ça fait des calculs plus simples (une solution ici, c'est le TD 7 d'analyse complexe).

[JJa]

Bonjour,

Il y a de quoi bien s'amuser avec les racines de l'équation tg(x)=x
En notant x(n) la n.ième racine (hormis la racine triviale x=0) :
x(n) = (2n+1)(pi/2) -u -(2/3)(u^3) -(13/15)(u^5) -(146/105)(u^7) -(781/315)(u^9) +O(u^11)
ceci avec u = 2/(pi(2n+1))
Autre propriété : Somme de (1/x(n))^p pour n =1 à infini est égale à :
(1/10) si p=2
(1/350) si p=4
(1/7875) si p=6
La fonction de Langevin (en particulier dans théorie des diélectriques) est développée en série en faisant intervenir les x(n) :
1/(coth(z)-(1/z)) = (3/z)+2z*somme de 1/((z^2)+(x(n)^2)) pour n=1 à infini.
Les racines x(n) correspondent aussi aux zéros de certaines fonctions de Bessel (sphérique de première espèce).
Il existe probablement d'autres propriétés remarquables...

[skilveg]

Salut,

Tu as une référence pour tous ces résultats?

[JJa]

Ce n'est pas une référence qu'il faudrait pouvoir fournir, mais au moins une dizaine !
Le développement en série des racines de tg(x)=x se trouve dans la plupart des handbooks de maths. Par exemple, voir :
http://mathworld.wolfram.com/TancFunction.html
Pour la somme des puissances paires des racines, c'est une note ancienne, mais je ne me souviens pas d'où elle provient. Il faudrait faire quelques recherches bibliographiques.
Pour les propriétés de la fonction de Langevin, c'est clairement une note prise autrefois dans des cours d'électrotechniques.
Désolé pour cette réponse vague : Je me réfère à des notes personnelles datant d'un lointain passé estudiantin. Je ne vous en ai fait part pour succiter la curiosité sur ce sujet qui m'avait intéressé à l'époque.

[skilveg]

Bonsoir,

Pythales, tu as prouvé que toutes les solutions étaient réelles ou non?

Jja, c'est bizarre, les premiers dénominateurs (10, 350, 7875) des sommes ne font pas partie de l'encyclopédie des suites d'entiers... Est-ce que tu as d'autres termes? Peut-être ne sont-ils pas tous entiers?

[JJa]

Bonjour,
je ne crois pas que les termes de la suite soient systématiquement les inverses de nombres entiers :
(1/10) , (1/350) , (1/7875), (37/6063750), ...
Cette 4ième fraction n'est pas prouvée analytiquement (à ma connaissance). C'est une conjecture personnelle confortée par calcul numérique.

[skilveg]

Après calculs, voici quelques valeurs probables des sommes des inverses des puissances -ièmes:

:
:
:
:

[mathelot]

bonjour,

est-ce qu'il y a un lien avec les nombres de Bernoulli ? (qui participent
au DSE de tangente )