Exo vecteurs

par **mellany-h** » 15 Aoû 2009, 12:45

Salut,

J'ai besoin d'un petit coup de main car je ne me rappelle plus la formule qui consiste à calculer des longueurs vectorielles.

Voici la question:
Dans un repère orthonormal (O;i ;j ) on considère les points suivants : A ( 2 ; 2) ; B (5 ; 6) ; C (4 ; 1).
Calculer les longueurs AB, AC et BC.

Merci d'avance.

par **struett** » 15 Aoû 2009, 12:53

Bonjour,

Je te conseille de faire un dessin de la situation. Tu te rendras peut-être compte après, que tu peux utiliser un théorème très célèbre que nous devons à un grec ayant vécu environ en 500 av JC pour trouver la distance qui sépare deux points.

en espérant que ça t'aide ;-)

Struett

par **mellany-h** » 15 Aoû 2009, 12:56

non je ne peux pas utiliser pythagaore puisque je n'ai aucune longueur, seulement des coordonées. De plus je dois utiliser des calculs vectoriels.

par **Ericovitchi** » 15 Aoû 2009, 13:01

Tu vas bien être obligé d'utiliser Pythagore :+++: . Si un vecteur

a pour coordonnées a et b alors la longueur du vecteur vaut

.
(et les coordonnées d'un vecteur sont calculées en prenant les coordonnées du point d'arrivée moins les coordonnées du point de départ).

par **mellany-h** » 15 Aoû 2009, 13:05

ça y est je me souviens. merci beaucoup

par **mellany-h** » 15 Aoû 2009, 13:19

Petit soucis.
Je crois avoir fait une erreur quelque part car je me retrouve qu'avec des racines.

par **struett** » 15 Aoû 2009, 13:20

Je comprends ta répulsion à l'idée d'utiliser pythagore^^

Je trouve qu'elle montre ta rigoureusité (ça ne se dit pas je crois... :hein: ) et c'est bien ! ^^

Mais il faut en fait voir les coordonnées comme des unités de longueur. En fait si on te donne les coordonnées (3,5) par exemple cela signifie 3 fois la longueur de

dans la direction de

et 5 fois la longueur de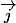

dans la direction de

.

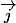Maintenant, ton repère est dit orthonormal ce qui signifie, entre autre, que les longueurs de

et de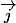

sont les mêmes et qu'elles sont égales à 1. Mais 1 quoi ? me demanderas-tu.

Eh ben en fait, c'est égal. si tu décide que l'unité est en cm, alors, tu auras une graduation en cm sur tes axes et les coordonnées (3,5) signifieront 3cm horizontalement et 5 cm verticalement. Et alors, tu as bien des "distances" et tu peux appliquer le théorème de pythagore. Maintenant, si tu décides que l'unité est le km, alors, tu auras une graduation sur tes axes et la coordonnée (3,5) signifiera 3 km horizontalement et 5 km verticalement. De nouveau tu as une distance et tu peux appliquer le théorème de pythagore.

Même si concrètement, tu trouveras deux longueurs différentes, à chaque fois il n'y a que les nombres 3 et 5 qui interviennent, et tu trouveras deux fois le même nombre pour la longueur seulement avec un ordre de grandeur différent.

Je me rends compte que mon blabla est long en fait. J'espère que ça t'aide quand même^^. Et sinon, je suis désolé, j'essaierais de te l'expliquer une deuxième fois différemment.

Struett

par **mellany-h** » 15 Aoû 2009, 13:25

Houla, j'ai rien compris.

par **struett** » 15 Aoû 2009, 13:32

Hum j'en suis désolé^^'

Je te propose donc d'oublier ce que j'ai dit en haut car je me dis aussi avec le recul que la formulation est particulièrement maladroite ^^'

faisons plus simple:

Tu dis que les coordonnées ne sont pas une distance. Mais en fait, on peut les interpréter comme une distance. Car les coordonnées nous indiquent les distances sur l'axe horizontal et sur l'axe vertical.

Si tu fais comme si les coordonnes de ton vecteur

sont des distances. (donc a est une distance; b est une distance), tu trouveras avec le théorème de pythagore une distance. Cette distance est la longueur qu'on parcourrait sur un axe parallèle au vecteur.

Est-ce que c'est plus clair?

Exo vecteurs

exo vecteurs

Qui est en ligne