Calculs limites de tendances

[MaudMC95]

Bonjours à tous,

étudiante en master j'ai un mémoire à rendre en septembre, mais j'ai eu mon sujet il y a 3 semaines, c'est un peu short.

le problème est le suivant:
j'ai une série de résultats analytiques pour le dosage d'une molécule X dans 50 lots d'un produit Y. Je dois déterminer quelles sont les limites supérieures et inférieures de tendances, dans le but final de déterminer quels sont les résultats hors tendances.

Selon un des seuls articles que j'ai pu trouver sur internet, il faut dans un premier temps que je vérifie que mes résultats suivent une Loi Normale. Pourquoi? et que se passe t-il si ce n'est pas le cas?

Dans un second temps je cherche à déterminer quelles sont les valeurs aberrantes. J'ai utilisé le test Q de Dixon et le test de Grubbs, est ce que j'ai bien fait? sinon que me conseillez vous?

merci d'avance pour vos réponses
amicalement
Maud

[WIWIWI]

Salut Maud,

La modélisation de ton problème se résume ainsi : tu as une variable aléatoire (v.a.) X="dosage de la molécule X dans Y" dont tu possèdes 50 réalisations, non? On suppose qu'elle suit une loi de probabilité. Or, quelle peut bien être cette loi de probabilité?
Il est courant, surtout dans ce genre de modélisation, de supposer que cette loi est une loi normale (ou également de Student) mais ce n'est pas forcément la "vrai" loi de cette variable aléatoire car personne, à part dieu s'il existe, ne la connait.
Donc il faut quantifier la validité de cette supposition : d'où les tests de normalité (voir Shapiro par exemple). Lorsque tu as validé cette supposition en acceptant l'hypothèse de normalité avec une probabilité assez forte, tu peux déterminer un intervalle de confiance de ta v.a. : par exemple, 95% des réalisations d'une v.a. normale N(m,s^2) sont comprises dans [q1=m-1.96*s,q2=m+1.96*s] avec q1 et q2 les quantiles à 2.5% et 97.5% respectivement.
Si tu recherches un intervalle de confiance pour la tendance du dosage et si tu est dans le cas de échantillons suivant une loi normale N(m,s^2), tu as la magnifique propriété que la moyenne de cette loi (et donc la tendance du dosage) suit une loi de student(m,s/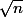). Ce qui te permet au passage d'avoir un intervalle de confiance pour la moyenne de la loi normale et donc des valeurs extrèmes pour la tendance du dosage.

En espérant t'avoir aiguillée.
A plus