Théorème de la fonction inverse

[marius1986]

Bien, bonjour a tous,
J'aimerai avoir des indications sur la démonstration du théorème de la fonction inverse (Dans un espace vectoriel de dimension finie n et muni d'un produit scalaire)
Merci d'avance

[prody-G]

salut !

Tu entends quoi par théorème de la fonction inverse ? c'est quoi l'énoncé ?

[mathelot]

Bonjour,

Il y a plusieurs théorèmes et idées dans ce domaine:

- les fonctions implicites
une relation où est une fonction suffisamment régulière définit localement z=f(x,y) comme fonction de x et y.

- la réciproque
une fonction f localement injective et de classe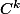 (k fois continuement dérivable) admet localement une bijection réciproque.
Celle-çi récupère les propriétés de f. Il s'agit d'un théorème utilisant beaucoup
de topologie (espace localement compact, théorème de l'application contractante).

Il me semble que l'on démontre tout cela en considérant les fonctions
comme point fixe d'opérateurs contractant bien choisis.

L'idée est de montrer que l'apllication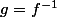 a les mêmes
propriétés que celles de f (continuité,dérivabilité..)

si et sont toutes les deux continues,
ce sont des homéomorphismes

si et sont toutes les deux continuement dérivables,ce sont des difféomorphismes

[marius1986]

Voici l'énoncé du théorème de fonction inverse
Soient E et F deux espaces de Banach, U un ouvert de E, a un point de U et f une application de classe .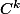
Pour qu'il existe un voisinage A de a tel que la restriction de f à A soit un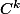 -difféomorphisme il faut et il suffit que f'(a) soit inversible.

Merci encore pour vos indications

[Arkhnor]

Salut.

Certains l'appellent théorème d'inversion locale, ou encore théorème de la bijection locale.

Tu peux trouver sa démonstration dans des livres comme Analyse réelle de S.Lang, ou Cours de Calcul Différentiel de H.Cartan.

Si tu cherches une preuve en dimension finie, tu peux surement trouver ton bonheur dans un livre de premier cycle.

La preuve utilise le théorème du point fixe pour les applications contractantes. (d'où l'importance que l'espace soit complet)

Voilà un lien où il est démontré : http://perso.univ-rennes1.fr/karim.bekka/CDHO/Week%20by%20week/CDHO5.pdf.
C'est cependant traité dans le cadre des espaces de Banach, il me semble que la preuve en dimension finie est légèrement plus simple.

:happy3: