Suite périodique

par **jeje56** » 06 Aoû 2009, 15:09

Bonjour,

Je dois montrer que toute suite périodique non constante diverge, je pense raisonner par l'absurde mais je bloque :

Soit u_n telle que :

Merci de votre aide !

par **prody-G** » 06 Aoû 2009, 15:35

Salut,

Oui l'absurde c'est le plus simple. Reviens à la définition de la divergence. Prends un A>u_0 par exemple et regarde ce que ça implique.

PS : es-tu sûr de la définition de ta suite parce qu'elle semble étrage :id:

par **leon1789** » 06 Aoû 2009, 15:57

Tout dépend ce qu'on appelle "raisonner par l'absurde"...

Personnellement, je dirais que dans une suite p-périodique avec

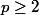
, on peut trouver facilement 2 sous-suites (constantes !) ayant des limites différentes... Donc, en vertu (de la contraposée) d'un théorème bien connu, une telle suite ne peut pas avoir de limite ...ce qui, en toute rigueur, est plus fort (EDIT : plus précis) que diverger !

par **Nightmare** » 06 Aoû 2009, 16:08

Salut,

Pour s'en sortir avec ce genre d'exercice il faut juste voir ce qu'il se passe (faire un dessin si nécessaire).

Regardons ce qu'il se passe dans le cas où il y a convergence vers un réel l arbitraire: On va pouvoir à partir d'un certain rang rendre la suite aussi proche de l, et même plus fort que ça, à partir d'un certain rang les termes de la suite vont rester aussi proche de l que l'on veut. (à ne pas oublier dans la définition de convergence)

A partir de là, où est le soucis? Si la suite était périodique, à partir d'un certain nombre d'itération on doit revenir sur les termes de la suite déjà obtenus. A la vue de ce que j'ai écris au dessus, cela voudrait donc dire que tous les termes de la suite sont contenus dans ce voisinage de l choisit arbitrairement (puisqu'à partir d'un certain rang la suite stagne dans ce voisinage). Il suffit alors de choisir un voisinage de l qui ne contienne pas au moins un terme de la suite (pourquoi peut-on le faire?), on obtient une absurdité.

par **jeje56** » 06 Aoû 2009, 16:10

Le théorème :
Toute suite extraite d'une suite convergente converge vers la même limite

Mais la contraposée prouve juste la divergence non ?
S'il existe deux suites extraites convergeant vers des limites différentes, alors u_n ne converge pas... donc diverge

Qu'en penses-tu léon ?

par **leon1789** » 06 Aoû 2009, 16:51

jeje56 a écrit:Le théorème :
Toute suite extraite d'une suite convergente converge vers la même limite

Mais la contraposée prouve juste la divergence non ?

Ce que tu dis est exact.

jeje56 a écrit:S'il existe deux suites extraites convergeant vers des limites différentes, alors u_n ne converge pas... donc diverge
Qu'en penses-tu léon ?

Personnellement, je dirais :
S'il existe deux suites extraites convergeant vers des limites différentes, alors u_n ne possède pas de limite... donc diverge

Théorème (similaire au tien) :
Toutes les suites extraites d'une suite possédant une limite ont la même limite.

Ici, deux suites extraites de limites différentes (comme le suggère Nigthmarre, faire un dessin d'une suite périodique) montrent que la suite n'a pas de limite.

par **jeje56** » 06 Aoû 2009, 17:24

Je vois, merci léon, Nightmare et Prody-G.

et

semblent être deux suites extraites constantes de limites différentes...

Merci !

par **leon1789** » 06 Aoû 2009, 17:35

jeje56 a écrit: et semblent être deux suites extraites constantes de limites différentes...

pas toujours : par exemple

puis "périodicité" :

C'est une suite 4-périodique, il faut prendre

et

par exemple.

Comme ta suite n'est pas constante, il existe deux éléments

,
puis deux sous-suites constantes

et

...

par **jeje56** » 06 Aoû 2009, 17:45

leon1789 a écrit:Personnellement, je dirais :
S'il existe deux suites extraites convergeant vers des limites différentes, alors u_n ne possède pas de limite... donc diverge

Avec mon théorème, on a directement la divergence non ? ^^

par **leon1789** » 06 Aoû 2009, 17:48

jeje56 a écrit:Avec mon théorème, on a directement la divergence non ? ^^

oui, pas de doute.

(mais "ne pas avoir de limite" est plus précis que "diverger")

par **jeje56** » 06 Aoû 2009, 17:51

Mais ton théorème m'a permis de rassembler les théorèmes :

u_n converge => toutes ses suites extraites convergent vers la même limite
et
u_n diverge vers l'infini => toutes ses suites extraites tendent vers l'infini

Merci pour le contre-exemple 1121,1121... ;-)

par **Nightmare** » 06 Aoû 2009, 19:04

Que dire des réciproques? :lol3:

par **jeje56** » 06 Aoû 2009, 19:21

La première est vraie ^^ : il suffit de choisir la suite extraite u(phi(n)) avec phi(n)=n pour tout n...

par **Nightmare** » 06 Aoû 2009, 19:30

Et en changeant un peu l'énoncé :

On suppose que si les suites extraites convergent, elles convergent toutes vers la même limite. (Un) converge-t-elle? ;)

par **jeje56** » 06 Aoû 2009, 19:34

Pas nécessairement : il peut alors exister une suite extraite divergente => u_n diverge

La négation de "toutes les suites extraites convergent vers la même limite" est "il existe deux suites extraites convergeant vers des limites différentes" OU "il existe une suite extraite divergente"...

non ?

par **Nightmare** » 07 Aoû 2009, 00:38

Ta première proposition ! Donc ta démo n'est pas bonne :lol3:

Il s'avère que dans certains cas (un métrique compact par exemple), l'unicité de la valeur d'adhérence implique la convergence de la suite.

par **jeje56** » 07 Aoû 2009, 07:42

J'ai peur de n'avoir pas compris ton deuxième énoncé...

Tu as changé :
Toutes les suites extraites convergent vers une même limite => u_n converge
en
Si toutes les suites extraites convergent alors elles convergent vers une même limite => u_n converge...

C'est bien ça ?

Pourquoi ma démo est fausse ?

Merci !

par **xyz1975** » 07 Aoû 2009, 07:55

J'ai pas tout lu mais je peux dire :

Une suite est convergente alors toutes ses sous suites (ou alors ses uites extraites) sont convergentes vers cette limite.

La réciproque :

1/ S'il existe une sous suite qui diverge alors la suite entière est divergente.

C'est équivalent à dire :

2/ S'il existe deux sous suites qui

vers deux limites différentes alors la suite entière ne peux pas admettre de limite.

par **leon1789** » 07 Aoû 2009, 09:21

"converger" et "avoir une limite" ne signifient pas tout à fait la même chose.
et "réciproque" et "contraposée" ne sont pas à confondre !

xyz1975 a écrit:J'ai pas tout lu mais je peux dire :

Si une suite est convergente alors toutes ses sous suites (ou alors ses suites extraites) sont convergentes vers cette limite.

La réciproque :

1/ S'il existe une sous suite qui diverge alors la suite entière est divergente.

Non, ceci n'est pas la réciproque !

La réciproque est :
Si toutes les sous-suites convergent alors la suite converge.
(ce qui est une trivialité puisque la suite elle-même est une sous-suite)

xyz1975 a écrit:C'est équivalent à dire :

2/ S'il existe deux sous suites qui tendent vers deux limites différentes alors la suite entière ne peut pas admettre de limite.

Ceci est la contraposée de :
Si une suite possède une limite alors toutes ses sous-suites tendent vers cette limite. (pas d'histoire de convergence ici)

Suite périodique

Suite périodique

Qui est en ligne