Convergence d'une série.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
prody-G
- Membre Relatif
- Messages: 376
- Enregistré le: 28 Mar 2006, 14:36
-
 par prody-G » 03 Aoû 2009, 15:36
par prody-G » 03 Aoû 2009, 15:36
Bonjour !
Je suis en train de me prendre la tête sur un question de développement limité et je n'arrive pas à voir où je me suis trompé !
On considère

et pour n>1 on pose
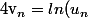-ln(u_{n-1}))
.
On veut le développement limité de

.
Je trouve
)
.
On demande d'en déduire que
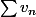
est convergente, mais je n'arrive pas à le montrer avec mon équivalent.
(c'est extrait de
capes sujet 1 2009 )
voilà, merci pour votre aide :id:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 03 Aoû 2009, 15:42
par Nightmare » 03 Aoû 2009, 15:42
Salut,
Revois ton développement asymptotique, il est clairement faux, ta suite devrait converger vers 0.
-
prody-G
- Membre Relatif
- Messages: 376
- Enregistré le: 28 Mar 2006, 14:36
-
 par prody-G » 03 Aoû 2009, 15:46
par prody-G » 03 Aoû 2009, 15:46
hehe ça y est merci nightmare j'ai vu mon erreur !
-
prody-G
- Membre Relatif
- Messages: 376
- Enregistré le: 28 Mar 2006, 14:36
-
 par prody-G » 03 Aoû 2009, 16:12
par prody-G » 03 Aoû 2009, 16:12
j'en profite pour poser une autre question :id:
le critère de riemann est équivalent-il à "si
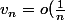)
alors
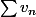
converge" ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 03 Aoû 2009, 16:24
par Nightmare » 03 Aoû 2009, 16:24
Euh déjà, es-tu sûr de ton :
"Si
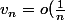)
alors
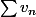
converge" ?
-
prody-G
- Membre Relatif
- Messages: 376
- Enregistré le: 28 Mar 2006, 14:36
-
 par prody-G » 03 Aoû 2009, 16:31
par prody-G » 03 Aoû 2009, 16:31
non justement, j'essaie de trouver un contre exemple mais sans succès, c'est pour ça que je demande ^^'.
En fait je me suis dit que puisqu'une série de Riemann

converge ssi
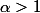
, ça veut dire qu'il suffit d'être juste un peu plus "docile" que
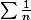
pour que ça marche. Voilà pourquoi je demande pour les
)
.
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 03 Aoû 2009, 16:43
par skilveg » 03 Aoû 2009, 16:43
Qu'est-ce que tu dis de la série

?
-
prody-G
- Membre Relatif
- Messages: 376
- Enregistré le: 28 Mar 2006, 14:36
-
 par prody-G » 03 Aoû 2009, 16:45
par prody-G » 03 Aoû 2009, 16:45
skilveg a écrit:Qu'est-ce que tu dis de la série

?
je dis merci ! j'y avais pas pensé :id:
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 03 Aoû 2009, 16:53
par skilveg » 03 Aoû 2009, 16:53
C'est un cas d'application du [url=http://fr.wikipedia.org/wiki/Séries_de_Bertrand]critère de Bertrand[/url], qui peut lui aussi se démontrer par comparaison série - intégrale.
-
xyz1975
- Membre Rationnel
- Messages: 555
- Enregistré le: 15 Sep 2007, 21:30
-
 par xyz1975 » 03 Aoû 2009, 17:29
par xyz1975 » 03 Aoû 2009, 17:29
Une condition suffisante (non nécessaire) pour que la série
)
est que la série

soit absolument convergente.
-
xyz1975
- Membre Rationnel
- Messages: 555
- Enregistré le: 15 Sep 2007, 21:30
-
 par xyz1975 » 03 Aoû 2009, 17:32
par xyz1975 » 03 Aoû 2009, 17:32
skilveg a écrit:C'est un cas d'application du [url=http://fr.wikipedia.org/wiki/Séries_de_Bertrand]critère de Bertrand[/url], qui peut lui aussi se démontrer par comparaison série - intégrale.
tu veux dire série ou intégrale de Bertrand pas critère, que beaucoup de prof dans les écoles préparatoires refusent de la considérer comme série (ou intégrale) de référence (je comprends pas pourquoi) alors que celle de Riemann n'est qu'un cas particulier.
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 03 Aoû 2009, 18:32
par skilveg » 03 Aoû 2009, 18:32
xyz1975 a écrit:tu veux dire série ou intégrale de Bertrand pas critère
Non non, c'est bien ce que je voulais dire... D'ailleurs je n'étais pas au courant de ce que tu dis sur la position des profs de prépa vis-à-vis de ce genre de séries. Pour moi c'était quasiment du cours.
-
xyz1975
- Membre Rationnel
- Messages: 555
- Enregistré le: 15 Sep 2007, 21:30
-
 par xyz1975 » 03 Aoû 2009, 18:36
par xyz1975 » 03 Aoû 2009, 18:36
skilveg a écrit:Non non, c'est bien ce que je voulais dire... D'ailleurs je n'étais pas au courant de ce que tu dis sur la position des profs de prépa vis-à-vis de ce genre de séries. Pour moi c'était quasiment du cours.
Je ne suis pas mieux placé que toi, mais ce n'est pas un critère mais c'est une série ou intégrale de référence, comme celle de Riemann mais pas un critère comme celui de D'alambert ou de Duhamel, n'est ce pas?
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 03 Aoû 2009, 18:40
par skilveg » 03 Aoû 2009, 18:40
Pour moi un critère c'est une condition suffisante, voire nécessaire et suffisante. Après, on peut jouer sur les mots comme on veut...
 par alavacommejetepousse » 03 Aoû 2009, 20:59
par alavacommejetepousse » 03 Aoû 2009, 20:59
bonsoir
pour moi ( et j'espére pour le plus grand nombre) un critère est une condition suffisante
une CNS est pour moi ( et j'espére...) une caractérisation
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 04 Aoû 2009, 06:47
par skilveg » 04 Aoû 2009, 06:47
Une CNS est en particulier suffisante, donc un critère... :marteau:
 par alavacommejetepousse » 05 Aoû 2009, 07:22
par alavacommejetepousse » 05 Aoû 2009, 07:22
skilveg a écrit:Une CNS est en particulier suffisante, donc un critère... :marteau:
si tu veux ... mais donne moi un exemple où on parle de critère pour une CNS ( évite de me taper sur la têteelleest fragile)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 18 invités
