Tant que j'y suis, est-ce que vous connaissez la forme d'une fonction harmonique radiale ? J'ai trouvé
Fonctions C²
28 messages
- Page 2 sur 2 - 1, 2
Pour un exercice comme celui que tu nous as posé, essaie de te représenter les choses dans l'espace.
Regarde :
on avait
 \in \mathbb{R}^2, f(x,y) = F(\sqrt{x^2+y^2})) (pense à un point
(pense à un point  du plan
du plan ) , de coordonnées
, de coordonnées ) :
:  est fonction de la distance de
est fonction de la distance de  à l'origine),
à l'origine),
et on a montré que ça impliquait que
 \in \mathbb{R}^+ \times [0,2 \pi], f(\rho \cos(\theta),\rho \sin(\theta)) = F(\rho)) (maintenant qu'on a changé le système de coordonnées, on peut "bloquer" l'angle, puisque celui-ci ne fait pas varier la distance de
(maintenant qu'on a changé le système de coordonnées, on peut "bloquer" l'angle, puisque celui-ci ne fait pas varier la distance de  à l'origine),
à l'origine),
donc en prenant en particulier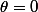 :
:
 = F(\rho)) (on se focalise sur la droite d'équation
(on se focalise sur la droite d'équation 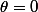 , dans le plan
, dans le plan ) : l'axe des abscisses).
: l'axe des abscisses).
Comme est
est  sur tout
sur tout  , elle l'est en particulier sur cette droite, et donc, comme elle y est égale à
, elle l'est en particulier sur cette droite, et donc, comme elle y est égale à  ,
,  est aussi
est aussi  !
!
Est-ce que tu comprends un peu mieux ?
PS : je n'ai pas consideré le problème en) , pour ne pas alourdir les choses.
, pour ne pas alourdir les choses.
Sinon, je n'ai jamais entendu parler des fonctions harmoniques radiales.
Regarde :
on avait
et on a montré que ça impliquait que
donc en prenant en particulier
Comme
Est-ce que tu comprends un peu mieux ?
PS : je n'ai pas consideré le problème en
Sinon, je n'ai jamais entendu parler des fonctions harmoniques radiales.
28 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
