Fonctions C²

[flo22]

Bonjour à tous,

J'ai et je dois montrer que f est C² ssi F est C².
Je suppose F C² et pose . Je dis que f=Fov et donc, F et v étant C², f est aussi C².

Mon raisonnement est-il bon pour l'instant ?

Merci.

[Maks]

Tu es sûr que est ?

[girdav]

Bonjour .
n'est pas en .

[Maks]

Roo !!! Laisse chercher :mur:

[flo22]

Oui oui ne vous inquiétez pas, j'ai oublié de le préciser (non en fait j'ai eu la flemme ^^), , on enlève bien le point (0,0)

[girdav]

Dans ce cas ça doit marcher.

[Maks]

Tu vas peut-être trouver ça chiant, mais, en mathématiques, il est important de toujours donner toutes les hypothèses, même sur un forum (d'ailleurs t'as dû voir nos poils se hérisser :marteau: ) ... Enfin bref, évite de refaire ça ...
Sinon, ton raisonnement est correct jusque là.

[flo22]

OK au temps pour moi :s
L'autre sens de l'équivalence me pose plus de problème. D'un coté ça m'a l'air "évident", mais en même temps je vois pas trop comment le formaliser...

[Maks]

Peut-être un petit passage en polaires, non ?

[flo22]

oula ! Jamais j'aurai penser à ça...

on a donc
Je dois faire un peu comme pour l'autre implication ? Composer pour arriver à f o...=F ?

[Maks]

Non, je crois que tu ne t'en sortira pas ainsi. Essaie plutôt de revenir à la définition de la classe , étape par étape (il y a peut être plus simple, mais là je vois pas).

[flo22]

Il faut donc que je montre que F est dérivable deux fois que que F'' est continue. Mais je ne peux pas calculer F' sans avoir montré avant qu'elle existe. Il ne faut quand même pas revenir à la définition de dérivabilité ???

[Maks]

Ben tu sais quand même des choses sur , qui devraient t'éviter de refaire tout le travail. Essaie de montrer que la fonction à gauche du signe égal est dérivable par rapport à , en utilisant le caractère de .

[flo22]

est donc dérivable par rapport à et non ?

[Oxypi]

Être de classe n'a pas de sens tout seul. On est de classe sur un ensemble (ouvert !) à préciser.

[Oxypi]

oula ! Jamais j'aurai penser à ça...

on a donc
Je dois faire un peu comme pour l'autre implication ? Composer pour arriver à f o...=F ?

Puisque est quelconque, pourquoi ne pas prendre une valeur en particulier ?

[flo22]

varie sur , pour chaque (x,y) il y a un différent non ?
Et je ne vois pas comment à partir d'une valeur montrer qu'une fonction est !? :hein:

[Oxypi]

Puisque c'est la fonction de la seule variable qui t'intéresse ici, tu peux fixer une valeur quelconque à puis utiliser le lien entre et pour conclure sur ton implication réciproque.

[flo22]

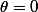
Evidemment, suis-je bête. Donc si je prends j'ai
Mais après ? (c'est là que je me rends compte que les fonctions à deux variables, j'y ai pas compris grand chose )

[Maks]

Ben à gauche tu as une fonction de , de classe , donc à droite aussi :ptdr: