Série et suite convergente
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
HC53
- Membre Naturel
- Messages: 22
- Enregistré le: 05 Mai 2008, 14:52
-
 par HC53 » 20 Juil 2009, 18:53
par HC53 » 20 Juil 2009, 18:53
bonjour,
on a la suite
)
définie par :
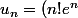/(n^n sqrt n))
et on a la suite auxiliare
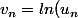-ln(u_{n-1}))
jai réussi a montré que la série
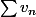
est convergente et je dois maintenant montré que la suite
)
converge
la série est convergente donc le terme général tend vers 0, on a donc l
-ln(u_{n-1}))
qui tend vers 0
est ce exact ? ensuite je ne vois pas comment continuer ?
merci pour votre aide
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 20 Juil 2009, 18:55
par Joker62 » 20 Juil 2009, 18:55
Haileau ;)
v_n est une série qu'on appelle téléscopique
écris v_n concrètement et voit ce qui se passe.
Les termes s'élimine deux à deux...
Edit : C'est pas v_n la série mais bon tu m'as compris...
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 20 Juil 2009, 18:57
par Pythales » 20 Juil 2009, 18:57
Par sommation,
-\ln(u_1))
Si
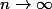
, cette quantité tend vers une limite finie, donc ...
-
HC53
- Membre Naturel
- Messages: 22
- Enregistré le: 05 Mai 2008, 14:52
-
 par HC53 » 20 Juil 2009, 19:03
par HC53 » 20 Juil 2009, 19:03
j'ai écrit concrètement
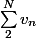
et je trouve :
+ln(u_N))
cad :
)
ensuite je dois faire tendre N vers l'infini
mais je ne vois pas comment dire que la suite (ln(u_n)) converge...
-
ToToR_2000
- Membre Relatif
- Messages: 121
- Enregistré le: 26 Juin 2009, 17:33
-
 par ToToR_2000 » 20 Juil 2009, 19:19
par ToToR_2000 » 20 Juil 2009, 19:19
Si tu n'arrives pas à le voir, c'est que tu n'as pas compris ce que signifie la convergence d'une série.
Poses-toi la question et après vérifie dans ton cours: tu pourras alors conclure sans difficulté.
-
HC53
- Membre Naturel
- Messages: 22
- Enregistré le: 05 Mai 2008, 14:52
-
 par HC53 » 23 Juil 2009, 15:40
par HC53 » 23 Juil 2009, 15:40
autant pour moi
merci pour votre aide j'ai compris !
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 24 Juil 2009, 09:44
par jeje56 » 24 Juil 2009, 09:44
Le résultat me paraît intuitif avec :
-ln(u_{n-1})\rightarrow 0)
qui ressemble au critère de Cauchy... Mais la démo proposée est mieux j'avoue ^^
On a donc
)_n)
qui converge, comment en déduire la convergence de
)
?
Merci !
-
Zavonen
- Membre Relatif
- Messages: 213
- Enregistré le: 23 Nov 2006, 10:32
-
 par Zavonen » 24 Juil 2009, 09:59
par Zavonen » 24 Juil 2009, 09:59
u_n=exp(log(u_n)) et exp est une fonction continue.
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 24 Juil 2009, 10:55
par jeje56 » 24 Juil 2009, 10:55
Exact :-) Merci à toi !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités