De la geométrie

par **darksoud** » 16 Juil 2009, 07:14

Bonjour,

Voici une petite énigme de géométrie.

Michel décide de fixer une antenne contre un mur.
Elle dispose donc d'une echelle de 6m. Mais un bloc de 1m sur 2m fait obstacle.
Il a cependant 2 façon de disposer son echelle pour pouvoir ainsi fixer son antenne.

Voir le dessin pour la disposition

Il nous faut déterminer x1 et x2 en cm

par **Maks** » 16 Juil 2009, 08:34

Bonjour. L'énoncé me semble incomplet. De plus, qu'as-tu fait ?

par **darksoud** » 16 Juil 2009, 08:39

Non l'énoncé est bien complet

par **Maks** » 16 Juil 2009, 08:42

Tu es sûr que tu n'oublies rien sur le schéma ?

par **darksoud** » 16 Juil 2009, 08:45

Non rien d'oublier sur le schéma.

par **Maks** » 16 Juil 2009, 08:50

Et bien on ne peut rien faire sans plus d'informations. Désolé.

par **darksoud** » 16 Juil 2009, 08:59

On sait que l'échelle mesure 6 mètre et qu'elle est posée sur un mur absolument vertical.
Elle s'appuie sur le mur, mais aussi sur le bord de l'obstacle, comme sur le schéma.
Il existe deux positions pour laquelle l'échelle touche le mur et le sol ainsi que le bord de l'obstacle.

par **Imod** » 16 Juil 2009, 22:08

Sauf erreur en observant les triangles rectangles semblables on aboutît à

et

sont les racines positives de l'équation

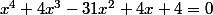
. Je n'ai pas trouver d'expression simple de ces racines .

Conclusion : rien de bien passionnant :triste:

Imod

par **darksoud** » 17 Juil 2009, 08:42

En effet la réponse n'est pas une expression simple.
Il peut y avoir des chiffres après la virgule ;)

par **nodjim** » 17 Juil 2009, 15:17

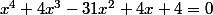
Imod a écrit:Sauf erreur en observant les triangles rectangles semblables on aboutît à et sont les racines positives de l'équation . Je n'ai pas trouver d'expression simple de ces racines .

Conclusion : rien de bien passionnant :triste:

Imod

ça me rappelle un certain camion qui voulait tourner dans un carrefour étroit genre couloir......

par **Imod** » 17 Juil 2009, 22:17

en effet il y a plusieurs variantes :

1°) Un camion ( ou une armoire ) de largeur

doit passer l'angle reliant deux rues ( couloirs ) de largeur

.

2°) Quelle est la longueur maximale d'une planche ( sans épaisseur ) pouvant venir à bout de l'angle droit formé par deux couloirs de largeurs

et

?

3°) On peut aussi prendre deux couloirs de tailles différentes dans 1°) ou ( ce qui revient au même ) donner une épaisseur à la planche du 2°) :mur:

Imod

De la geométrie

De la geométrie

Qui est en ligne