Zone à bâtir
Olympiades mathématiques, énigmes et défis

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 15 Juil 2009, 17:32
par Ericovitchi » 15 Juil 2009, 17:32
Un petit problème niveau lycée mais qui me plait bien :

Un champ a la forme d'un triangle rectangle. On doit y bâtir les deux zones en bleu suivant la géométrie décrite sur le dessin (mais on est maître des dimensions des rectangles).
Comment doit-on s'y prendre pour maximiser la zone bâtie ?
Et peut-on arriver à bâtir plus de la moitié de la surface du triangle ?
-
Anonyme
 par Anonyme » 15 Juil 2009, 17:42
par Anonyme » 15 Juil 2009, 17:42
Qu'est ce que tu veut dire par:
Ericovitchi a écrit:On doit y bâtir les deux zones en bleu suivant la géométrie décrite sur le dessin (mais on est maître des dimensions des rectangles).
C'est pas clair

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 15 Juil 2009, 18:01
par Ericovitchi » 15 Juil 2009, 18:01
On a la contrainte que les deux rectangles soient l'un au dessus de l'autre et c'est à peu près tout.
Après que l'un de leur coin touche l'hypoténuse et que leur coté droit touche le bord droit du triangle, c'est un conséquence du fait que l'on veut maximiser la surface.
-
guigui51250
- Membre Complexe
- Messages: 2727
- Enregistré le: 30 Déc 2007, 11:00
-
 par guigui51250 » 15 Juil 2009, 18:15
par guigui51250 » 15 Juil 2009, 18:15
Qmath a écrit:Qu'est ce que tu veut dire par:
C'est pas clair
Les deux rectangles sont dans le triangle, comme sur le dessin
-
ramon717
- Membre Naturel
- Messages: 15
- Enregistré le: 15 Juil 2009, 13:42
-
 par ramon717 » 15 Juil 2009, 18:40
par ramon717 » 15 Juil 2009, 18:40
tres interressant , je me demande si le meilleur moyen est d'equilbrer les 2 rectangle ou s'il faut en faire un seul qui prend le max d'espace et puis faire le deusieme en remplissant le maximum d'espace d'un des 2 coin restant , je suis nul en geo mais je vais my pencher , ça n'a pas l'air simple par le calcul en tout cas
premiere idée : la variable doit etre la position des coins sur l'hypotenuse , soit on met un a 1/2 et l'autre a 1/4 d'un d 2 coté , ou alors soit les 2 coins sont chacun a 1/3 de l'hypotenuse
pour la surface alors la ! faudrai voir une fois optimiser l'espace pris par les carré
edit : je croi qu'il est plus simple de chercher a minimiser les triangle restant

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 15 Juil 2009, 19:22
par leon1789 » 15 Juil 2009, 19:22
Il me semble que la solution ne dépend pas de la pente de l'hypothénuse du triangle, et qu'il s'agit toujours de "1/3 et 2/3" : on couvre ainsi deux tiers du triangle.

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 15 Juil 2009, 20:59
par Ericovitchi » 15 Juil 2009, 20:59
que ça ne dépende pas de la pente, c'est vrai
1/3, 2/3 c'est quoi ? c'est l'abscisse du début des rectangles ?
C'est pas faux, tu as trouvé ça comment ?
Couvrir les 2/3 du triangle ? alors là je ne suis pas d'accord.
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 15 Juil 2009, 21:12
par Imod » 15 Juil 2009, 21:12
En fait le problème revient à trouver le maximum de

avec

,

,

positifs et
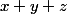
fixé . La logique voudrait que
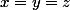
on a alors la partie bleue qui fait deux fois la verte .
Imod

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 15 Juil 2009, 21:14
par leon1789 » 15 Juil 2009, 21:14
Ericovitchi a écrit:que ça ne dépende pas de la pente, c'est vrai
1/3, 2/3 c'est quoi ? c'est l'abscisse du début des rectangles ?
oui, le premier rectangle commence au 1/3 de la base (et monte au 1/3 de l'hypothenuse, et au 1/3 du troisième coté aussi), le second rectangle commence au 2/3 de la base (et monte au 2/3 de l'hypothenuse, et au 2/3 du troisième coté aussi).
Ericovitchi a écrit: C'est pas faux, tu as trouvé ça comment ?
En mettant les choses en équation avec deux inconnues et une aire à maximiser... Bref, une traduction algébrique du problème.
Ericovitchi a écrit:Couvrir les 2/3 du triangle ? alors là je ne suis pas d'accord.
ah... on prend un triangle rectangle isocèle avec une base de longueur 3 ?
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 15 Juil 2009, 22:10
par Imod » 15 Juil 2009, 22:10
J'ai trouvé une petite démonstration géométrique ( sans aucun calcul ) qui répond aux deux questions , je vous laisse réfléchir un peu avant de joindre une illustration :zen:
Imod
-
ramon717
- Membre Naturel
- Messages: 15
- Enregistré le: 15 Juil 2009, 13:42
-
 par ramon717 » 16 Juil 2009, 02:57
par ramon717 » 16 Juil 2009, 02:57
je ne parlai pas de pente mais de la position du coin supérieur gauche des carrés (sur l'image donnée ici) sur l'hypoténuse , donc la bonne solution est le 1/3 1/3 , maintenant pourquoi ...
parceque plus on raproche les coins des carrés se trouvant sur l'hypoténuse des angles que forme l'hypoténuse , ou entre eux , plus on retréci l'aire des carrés , donc la plus grande surface des carrés sera donnée par une equirépartition (ça se dit ?) de leurs coins sur l'hypoténuse
ça marche ça ?
l'aire des carrés est égale aux 4/7 de l'aire du grand triangle
moi aussi sans calculs alors c'est peut être faux
edit : je trouve aussi 2/3 du grand triangle maintenant :mur:
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 16 Juil 2009, 21:58
par Imod » 16 Juil 2009, 21:58
Je vous laisse observer ces deux dessins :zen:


Imod

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 17 Juil 2009, 16:53
par Ericovitchi » 17 Juil 2009, 16:53
C'est très intéressant tes dessins. Déjà avec le premier le problème devient : Comment minimiser
)
sous la contrainte x+y+z=a ce qui simplifie le problème et le rend très symétrique :id:
Pour le second ou la comparaison des deux, j'ai moins bien compris.
Tu veux montrer que quand on enlève quelque chose à x alors il faut rajouter la même chose à y ?
Sinon traditionnellement la solution est :

Comment maximiser S1+S2 ?
On calcule
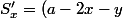tan(\alpha) = 0)
et
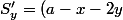tan(\alpha)=0)
qui a la solution x=a/3 et y=a/3 qui montre bien la géométrie des deux rectangles. Du coup S1+S2=
)
Et comme l'aire totale est
)
le ratio max de zone habité est de 2/3

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 17 Juil 2009, 17:11
par leon1789 » 17 Juil 2009, 17:11
Ericovitchi a écrit:(...) le ratio max de zone habité est de 4/9
ah... on prend un triangle rectangle isocèle avec une base de longueur 3 ?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 17 Juil 2009, 17:19
par leon1789 » 17 Juil 2009, 17:19
Imod a écrit:Je vous laisse observer ces deux dessins :zen:

Imod
En regardant ce dessin et en imaginant que l'on cherche un "point d'équilibre", on se dit qu'il faut que les 3 rectangles verts sur la diagonale soient isométriques, d'où "1/3, 1/3, 1/3". La surface bleue sera alors deux fois plus importante que la surface verte.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 17 Juil 2009, 17:24
par Zweig » 17 Juil 2009, 17:24
Ericovitchi a écrit:C'est très intéressant tes dessins. Déjà avec le premier le problème devient : Comment minimiser
)
sous la contrainte x+y+z=a ce qui simplifie le problème et le rend très symétrique :id:
Je n'ai pas regardé les autres messages du topic, mais

est-il donné ? Si oui, alors on minimise très facilement le produit
)
. D'après l'inégalité de Cauchy-Schwarz, on a :
 \geq \frac{ka^2}{3})
Le minimum est atteint lorsque

-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 17 Juil 2009, 17:30
par Imod » 17 Juil 2009, 17:30
Ericovitchi a écrit:Pour le second ou la comparaison des deux, j'ai moins bien compris.Tu veux montrer que quand on enlève quelque chose à x alors il faut rajouter la même chose à y ? ...
L'objectif du deuxième dessin est de montrer que pour
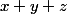
constant
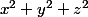
est minimum quand
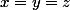
( les trois grandeurs étant positives ) . Si par exemple
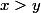
on diminue
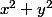
( donc

) en remplaçant

et

par la moyenne des deux (

et donc
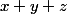
restant constant ) .
Imod
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 17 Juil 2009, 18:32
par nodjim » 17 Juil 2009, 18:32
Bonsoir à tous.
Ce serait bien plus drôle de savoir ce qui se passe si on met un 3ème rectangle, et un 4ème, et un 5ème...
Quel taux de remplissage max peut on espérer avec N rectangles?
Résultat simple.
Bon amusement à tous

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 17 Juil 2009, 19:37
par leon1789 » 17 Juil 2009, 19:37
nodjim a écrit:Quel taux de remplissage max peut on espérer avec N rectangles?
Résultat simple.
... (N-1)/N ?
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 17 Juil 2009, 22:25
par Imod » 17 Juil 2009, 22:25
nodjim a écrit:Bonsoir à tous.
Ce serait bien plus drôle de savoir ce qui se passe si on met un 3ème rectangle, et un 4ème, et un 5ème...
Quel taux de remplissage max peut on espérer avec N rectangles?
Résultat simple.
Bon amusement à tous
C'est un peu pour cette raison que j'aime bien proposer une solution purement géométrique à un problème purement géométrique ( les puristes parlent de démonstration synthétique ) . La démonstration que j'ai proposée s'adapte sans aucun effort à un nombre quelconque de rectangles :zen:
Imod
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 9 invités




