L'ensemble des applications

[armani]

Bonjour,
Un problème d'axiome en étudiant les Ensembles me tourmente:
"Les applications d'un ensemble A dans B forment un ensemble noté F(A, B)."

Celà veut-il dire que l'ensemble formé sont tous les images de tous les éléments de A dans B ?

Malgrè un exemple, je n'e saisi pas bien le sens:

"L'ensemble F({a}, B) est en bijection naturelle avec B par l'application f --> f(a) de F({a}, B) dans B. En effet connaître une application f de {a} dans B revient à connaitre l'image f(a)€B."

Le garçon paumé que je suis vous remerçie.

PS: je me base sur le livre "Mathématique tout en un pour la license (L1)" des éditions Dunod.

[Luc]

Salut,

Pour toi, qu'est-ce qu'une application de A dans B? Si tu le définis clairement, tout sera plus facile :)

Luc

[armani]

Une application est un procédé qui permet d'associer un élément d'un ensemble de départ A à un et un seul autre élément d'un ensemble d'arrivé B.

Donc l'ensemble F(A, B) représente t'il des éléments ?
Je retourne sans cesse mon cerveau et recherche en vain de comprendre ce fameux ensemble...

[leon1789]

Donc l'ensemble F(A, B) représente t'il des éléments ?

En tout cas, pas des éléments de B !

F(A,B), c'est l'ensemble de toutes les applications de A dans B.
Un élément est une application de f : A -> B.

[skilveg]

Une application est un procédé qui permet d'associer un élément d'un ensemble de départ A à un et un seul autre élément d'un ensemble d'arrivé B.

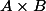
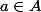
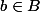
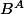
Et c'est quoi, la définition d'un procédé? :langue2: Mathématiquement, une application de dans est une partie de (le graphe de l'application) tel que pour tout , il existe un unique tel que . Du coup le fait que l'ensemble des applications de dans est bien un ensemble n'est pas vraiment un axiome (dans ZF, il me semble qu'il découle du schéma d'axiomes de substitution).

[armani]

:id: Ca m'est maintenant très clair.
MERCI !!!

[Zavonen]

Tu peux ici réviser toutes ces notions avec des exemples concrets:
Applications