Equation droite par symetrie

[zipei]

Bonjour !

Mes cours de maths etant lointain je ne sais plus tres bien faire ca, j'espere que vous pourrez m'aider !


J'ai deux droites y=ax+b et y=cx+d

Quelle est l'equation de la troisieme droite qui serait le symetrique de la premiere droite par rapport a la deuxieme ? (en gardant le meme repere)


D'avance merci pour vos reponses (et desole pour l'absence d'accents j'utilise un clavier qwerty...)

zipei

[sky-mars]

Salut
Je sais pas si c'est une bonne solution mais j'aurai pensé à la distance.
si
étant un point appartenant à la droite qu'on cherche.
On pourrait même prendre la norme au carrée pour s'affranchir de la racine.

[busard_des_roseaux]

Bj,

une droite (D) est définie par
un point A et un vecteur non nul qui
en donne sa direction.

une droite (D) d'équation y=ax+b
est dans la direction de

la pente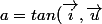

On cherche le point B à l'intersection de (D) et (D') en résolvant
le système


soit la direction horizontale
la symétrique D" est dirigée par tel que


égalité dans le groupe des angles orientés de droites (mod pi)

si la symétrique D" a pour équation y=mx+p

en passant aux tangentes avec la trigo:


d'où la pente m de D" en résolvant la dernière équation d'inconnue m.

[zipei]

Bonjour a vous deux et merci pour vos reponses !

Busard_des_roseaux, j'ai essaye ta methode mais elle ne fonctionne pas, ou plutot peut etre que je me suis trompe quelque part...
Je t'explique comment j'ai fait. En fait, j'ai une droite (correspondant a un rayon) qui croise une parabole, et je dois determiner le rayon incident. Pour cela, j'ai l'equation de ma parabole : y=a(x+b)^2, et une droite y=dx+e.
Je prend donc l'equation de la tangent au point d'intersection (le point d'intersection est appele X) ce qui donne : y=a(X+b)^2+2a(X+b)(x-X).
D'apres ta methode, je devrais trouver m en resolvant : (m+d)/(1-m*d)=(2*2a(X+b))/(1-(2a(X+b))^2)
Cependant en prenant des parametres arbitraires, et en faisant juste un graphique, je n'obtiens pas du tout la droite symetrique de la droite incidente par rapport a la tangente... Est ce que je me suis trompe quelque part ou... ?

sky_mars, ta methode a l'air interessante peux tu m'en dire un peu plus s'il te plait ?

[zerroudi]

Bonjour,

Soit M3 (point de la droite D3 recherchée) la symetrie de M1 (point de la droite D1) par rapport à D2. La projection de M1 sur D2 est notée M2.

L'équation de la droite D3 peut être obtenue à partir de l'équation suivante :
(*)

Pour la resoudre, il faut trouver .
Ce vecteur peut être trouver en dérivant par rapport à 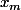où 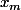est l'abscis de .

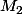Tu trouve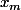 à l'aide de , tu remplace après dans puis dans (*).
Finalement, tu essayras de faire un changement de variable pour mettre sou sla forme