Petite application réelle des maths
14 messages
- Page 1 sur 1
Petite application réelle des maths
Bonjour
Je cherche à établir une loi qui régit ceci :
On démarre u(0)=1
Puis on constitue une suite selon un fait réel suivant :
Chaque personne rameute 2 personnes
Donc on a :
u(0)=1
u(1)=1+2=3
u(2)=3+2x2=7
u(3)=7+4x2=15
Etc..
Il semble se passer le phénomène suivant :
u(n+2)=u(n+1)+2x(u(n+1)-u(n))
soit u(n+2)-3xu(n+1)+2xu(n)=0
J'utilise mon cours avec l'équation caractéristique r²-3r+2 de racines 1 et 2 et je cherche des solutions en Aexp(2n)+Bexp(n)
Où est la faute ?
Merci
Je cherche à établir une loi qui régit ceci :
On démarre u(0)=1
Puis on constitue une suite selon un fait réel suivant :
Chaque personne rameute 2 personnes
Donc on a :
u(0)=1
u(1)=1+2=3
u(2)=3+2x2=7
u(3)=7+4x2=15
Etc..
Il semble se passer le phénomène suivant :
u(n+2)=u(n+1)+2x(u(n+1)-u(n))
soit u(n+2)-3xu(n+1)+2xu(n)=0
J'utilise mon cours avec l'équation caractéristique r²-3r+2 de racines 1 et 2 et je cherche des solutions en Aexp(2n)+Bexp(n)
Où est la faute ?
Merci
Flo38 a écrit:Bonjour
Je cherche à établir une loi qui régit ceci :
On démarre u(0)=1
Puis on constitue une suite selon un fait réel suivant :
Chaque personne rameute 2 personnes
Donc on a :
u(0)=1
u(1)=1+2=3
u(2)=3+2x2=7
u(3)=7+4x2=15
Etc..
Il semble se passer le phénomène suivant :
u(n+2)=u(n+1)+2x(u(n+1)-u(n))
soit u(n+2)-3xu(n+1)+2xu(n)=0
J'utilise mon cours avec l'équation caractéristique r²-3r+2 de racines 1 et 2 et je cherche des solutions en Aexp(2n)+Bexp(n)
Où est la faute ?
Merci
Bonsoir,
Tu peux trouver une définition plus simple de ta suite...
Flo38 a écrit:J'aimerais le faire comme ça en fait..Je me suis pas vraiment posé la question pour autrement mais je ne comprends pas que ça marche pas
Sinon pour la définition plus simple tu parles juste par récurrence simple ?
Où j'ai pensé aussi à la somme de la suite géométrique 2^n
Exactement ! C'est ainsi que la suite est construite...
Selon la première mise en équation la suite doit pouvoir se déterminer par récurrence double (même résolution que les équadiff du second ordre)
Seulement après résolution je constate que u(3) n'est déjà pas ce que je cherche..Et je ne comprends pas où je me trompe..
Je veux faire ça pour revoir un peu mon cours..
Seulement après résolution je constate que u(3) n'est déjà pas ce que je cherche..Et je ne comprends pas où je me trompe..
Je veux faire ça pour revoir un peu mon cours..
bonjour,
d'abord, apparament (ce que j'ai lu plus haut) c'est des equations que t'es entrain de resoudre qui te donnes cette suite . tu pourrais nous les poster ?
- pourquoi 4 ??? u(3) = 7 + 4*2.
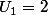 ce qui est faux ! et donc NON .
ce qui est faux ! et donc NON .
je cris pas victoir trop vite; faut attendre les equations sources. mais jusqu'à la
ça verifie la suite (BRAVO)
d'abord, apparament (ce que j'ai lu plus haut) c'est des equations que t'es entrain de resoudre qui te donnes cette suite . tu pourrais nous les poster ?
- pourquoi 4 ??? u(3) = 7 + 4*2.
"kazeriahm" a écrit:
"Black Jack" a écrit:
je cris pas victoir trop vite; faut attendre les equations sources. mais jusqu'à la
ça verifie la suite (BRAVO)
* In God we trust, for all others bring data *
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
