Irrationnel

[Anonyme]

Bonjour

Voici la démonstration de l'irrationalité de la racine carre d'un nombre premier

Soit un nombre premier et sa racine

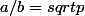
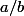
supposons que tel que soit la fraction la plus simplifiee

on élève le tout au carre on obtient alors

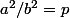
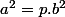
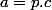
Par consequant est divisible par . Donc aussi est divisible par. On peut donc écrire , est un entier.

Ainsi
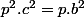
donc
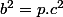
Pour les même raisons citées plus haut on trouve que est divisible par donc la fraction de départ ne peut pas être irréductible. c'est une contradiction avec l'hypothèse de départ donc cette fraction n'existe pas

Alors mes questions :
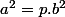
1/ Pourquoi si alors nécessairement divise ? Comment démontrer cela ?

2/ Si on avait posé au départ un nombre quelconque pas nécessairement premier, on aurais eu que est irrationnel alors que ce n'est pas toujours vrai. Comment est ce possible ?

Merci

[oscar]

Bonjour Voici un exemple avec V 2


http://img15.imageshack.us/i/racinede2irrationnel.jpg/

[Anonyme]

Je connais l'exemple avec , c'est l'exemple le plus facile d'ailleurs

Mais ce que je demande c'est ça:

Alors mes questions :
1/ Pourquoi si alors nécessairement divise ? Comment démontrer cela ?

2/ Si on avait posé au départ un nombre quelconque pas nécessairement premier, on aurais eu que est irrationnel alors que ce n'est pas toujours vrai. Comment est ce possible ?

Svp pour le 1/ ne me donner pas l'exemple ou p=2

Merci

[nuage]

Salut,
si alors divise par définition.
Par contre le fait que divise vient du fait que est premier. Par exemple 12 divise mais ne divise pas 6.

En tout état de cause la racine carré d'un entier naturel est soit entière soit irrationnelle.

[Zweig]

Le fait que se démontre via une décomposition en produits de facteurs premiers. Je ne sais pas si c'est très rigoureux, mais bon, c'est l'idée, je pense :



Comme et premier, alors il existe un indice tel que et tel que . Mais alors et comme , alors .

On montre, bien sûr, que plus généralement, pour tout naturel :

[Anonyme]

Salut,
si alors divise par définition.
Par contre le fait que divise vient du fait que est premier.

Justement comment demontrer cela ?
pourquoi quand est premier il divise s'il divise ?

Desole Zweig j'ai rien compris a ta démonstration (je suis en seconde et ça me depasse)

Quelqu'un pourrait-il demontrer d'une autre maniere ?

[pido]

bonjour
c'est banal de démontrer que si p divise donc p divise a.
car si p divise =a.a et p premier donc p divise a .

[nuage]

Salut pido

bonjour
c'est banal de démontrer que si p divise donc p divise a.
car si p divise =a.a et p premier donc p divise a .

C'est banal, mais pas évident : la démonstration (enfin l'idée) a été donnée par Zweig.
J'espère que tu ne penses pas en avoir donné une.

[Anonyme]

Salut pido

C'est banal, mais pas évident : la démonstration (enfin l'idée) a été donnée par Zweig.
J'espère que tu ne penses pas en avoir donné une.

Justement j'ai pas compris la demo de Zweig , cela dépasse mon niveau .

Pourrait -on demontrer cela autrement ?

[nodjim]

L'exemple 7.
Si 7 a un carré rationnel, il s'écrit a/b, a et b entiers.
(a/b)²=7
a²=7b²
A droite il y a 7 donc, il y a forcément au moins 1 "7" dans la décomposition de a. donc a s'écrit 7a
(7a)²=7b²
7²*a²=7 b²
il me manque un "7" à droite, il est dans la décomposition de b
Donc b s'écrit 7b.
7²*a²=7*(7b)²=7*7²*b²=7^3*b².
Bon, maintenant il manque un "7" à gauche.
Etc...
ça marche pour toute puissance, pas seulement les carrés.

[Anonyme]

L'exemple 7.
Si 7 a un carré rationnel, il s'écrit a/b, a et b entiers.

Tu ne voulais pas dire si 7 a une racine rationelle, ... ...

(a/b)²=7
a²=7b²
A droite il y a 7 donc, il y a forcément au moins 1 "7" dans la décomposition de a. donc a s'écrit 7a

Justement pourquoi ?

[Skullkid]

Salut, l'idée c'est que tu ne peux pas "couper" un nombre premier (par couper, je veux dire l'écrire comme produit de deux nombres autrement que 1 x p).

D'une manière générale, lorsque a divise le produit bc, on n'a pas forcément a divise b ou a divise c. Tout ce qu'on peut dire c'est qu'une "partie" de a divise b, et que l'autre divise c. Par exemple : 6 divise 12 = 4x3. On peut "couper" 6 en 3x2, et on a bien 2 divise 4 et 3 divise 3.

Mais dans le cas d'un nombre premier, comme tu ne peux pas le couper, il divise forcément l'un ou l'autre des termes du produit.

D'une manière plus rigoureuse, ça donne ce que t'a dit Zweig, à savoir que le nombre premier apparaît forcément dans la décomposition en facteurs premiers de b ou de c.

[pido]

salut Qmath
pour ta deuxieme question il faut bien noter que l'idée de base pour montrer que est irrationnel estl'absurde .la seconde idée importante pour le raisonnement c'est ce resultat vérifié seulement pour les nombres premiers :
p divise implique p divise a
je rappelle que c'est vérifié seulement car p est premier .

[pido]

pour l'intervention de nuage au sujet de mon raisonnement je vais dire que malgré que cela apparaisse simple mais c'est correcte.
car on a p divise et p premier donc p divise a ou a alors p divise a .il faut bien se rappeler :
p premier p divise ab implique p divise a ou b

[Anonyme]

Salut, l'idée c'est que tu ne peux pas "couper" un nombre premier (par couper, je veux dire l'écrire comme produit de deux nombres autrement que 1 x p).

D'une manière générale, lorsque a divise le produit bc, on n'a pas forcément a divise b ou a divise c. Tout ce qu'on peut dire c'est qu'une "partie" de a divise b, et que l'autre divise c. Par exemple : 6 divise 12 = 4x3. On peut "couper" 6 en 3x2, et on a bien 2 divise 4 et 3 divise 3.

Mais dans le cas d'un nombre premier, comme tu ne peux pas le couper, il divise forcément l'un ou l'autre des termes du produit.

D'une manière plus rigoureuse, ça donne ce que t'a dit Zweig, à savoir que le nombre premier apparaît forcément dans la décomposition en facteurs premiers de b ou de c.

Merci j'ai compris.