F periodique et constante

par **yutor** » 11 Fév 2006, 09:26

Bonjour à tous,

j'ai une fonction f définie et continue sur R,admettant a dans Q* et b dans R/Q comme périodes.

on me demande de démontrer que f est constante?

MERCI POUR VOS IDEES; :happy2:

par **redwolf** » 11 Fév 2006, 09:46

Bonjour.

Le sous-groupe de

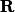
engendré par

et

est dense dans

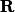
en raison des hypothèses faites sur

et

.

est continue et constante sur une partie dense, elle est donc constante.

par **yutor** » 11 Fév 2006, 09:54

Merci Redwolf Pour Ta Reponse

par **Mikou** » 11 Fév 2006, 11:09

au passage 'f est periodique et constante' est un non sens, non ? il me semble que l'on dit jms de f quelle est 0-periodique.

par **redwolf** » 11 Fév 2006, 13:25

Bonjour

Etre constante, ce n'est pas être 0-périodique. C'est être pour tout x x-périodique. Les fonctions constantes sont bien des fonctions périodiques.

par **Mikou** » 11 Fév 2006, 13:29

:hein: tu parles dune fonction x- ?

F periodique et constante

f periodique et constante

Qui est en ligne