Anneau

[arsene]

Bonjour
j aimerais montrer ceci
A et B ideaux maximaux d un anneau commutatif alors AB= A inter B
la deuxieme question porte sur les anneaux noetheriens.
Un epimorphisme d anneau noetherien est il injectif?
Sinon donnez moi un contre exple.
Je sais qu un epimorphisme d`anneau non notherien n est pas injectif.C dans le livre que jai vu l exple.Je suis donc tentée de dire oui a la deuxieme question mais pour la demo je ne trouve rien
Pour la 1ere
J etais tentée de me dire qu un ideal maximal n´est contenu dans aucun autre ideal si ce n est lui meme ou l anneau tout entier mais je crois que le livre ne donne pas des exos contraires aux definitions,Je dois surement pas avoir compris je suis sure.
merci d avance

[leon1789]

A et B ideaux maximaux d un anneau commutatif alors AB= A inter B

il faut montrer et

Une de ces deux inclusions est très simple : laquelle ?

la deuxieme question porte sur les anneaux noetheriens.
Un epimorphisme d anneau noetherien est il injectif?

pour toi, c'est quoi un épimorphisme ?

> : le même au départ et à l'arrivée,
ou pas ( > ) ?

[abcd22]

Bonjour,

la deuxieme question porte sur les anneaux noetheriens.
Un epimorphisme d anneau noetherien est il injectif?
Sinon donnez moi un contre exple.

Je rappelle les définitions :
Un morphisme est un épimorphisme si et seulement si pour tout anneau C et tous morphismes de B vers C, on a .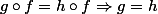
Un morphisme est un monomorphisme si et seulement si pour tout anneau C et tous morphismes de C vers A, on a .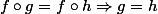
La notion d'épimorphisme correspond à la surjectivité dans la catégorie des ensembles, et celle de monomorphisme à l'injectivité, donc intuitivement (mais c'est vrai qu'il faut parfois se méfier de son intuition avec ce genre de choses), il n'y a aucune raison pour qu'un épimorphisme d'anneaux (noethériens ou pas) soit injectif (de la même façon qu'il n'y a aucune raison pour qu'une fonction surjective soit injective en général), et effectivement, la projection canonique de Z dans Z/2Z par exemple est un épimorphisme non injectif (et il n'y aussi aucune raison pour qu'un monomorphisme d'anneaux soit surjectif, contre exemple le morphisme de Z dans Z², (j'ai édité, ma première version était un morphisme de Z-modules mais pas d'anneaux...)).
Les questions intéressantes à se poser pour voir si les notions de monomorphisme et épimorphisme correspondent à notre intuition dans le cas des anneaux sont :
Un épimorphisme d'anneaux (noethériens) est-il surjectif ?
Un monomorphisme d'anneaux (noethériens) est-il injectif ?
Et la réponse est o;););)non à la première question, que les anneaux soient noethériens ou pas, et oui à la 2e, voir posts suivants.

[leon1789]

Autre question intéressante (et c'est pour cela que je demandais une précision sur l'énoncé) :
un épimorphisme d'un anneau sur lui-même est-il injectif ?

[abcd22]

Un épimorphisme d'anneaux (noethériens) est-il surjectif ?
Un monomorphisme d'anneaux (noethériens) est-il injectif ?
Et la réponse est oui aux deux questions (exercice : le montrer), que les anneaux soient noethériens ou pas.

Hum non, j'ai dit n'importe quoi, j'ai confondu les anneaux et les modules…
Dans la catégorie des modules sur un anneau A, les épimorphismes sont surjectifs et les monomorphismes injectifs, pour le voir on prend par exemple un épimorphisme f de A dans B, C = B/Im f, g = 0 et h la projection canonique de B dans C, la définition d'épimorphisme donne h = 0 d'où Im f = B; et pour les monomorphismes on prend C = Ker f, g = 0 et h l'inclusion de C dans A.
Et si on met des anneaux au lieu de modules ça ne marche plus car le noyau d'un morphisme d'anneaux n'est pas un anneau mais seulement un idéal, et l'image d'un morphisme d'anneaux n'est pas nécessairement un idéal de l'anneau d'arrivée donc B/Im f n'est pas forcément un anneau… Et la fonction nulle n'est pas un morphisme d'anneaux car l'image de 1 n'est pas 1.
Comme contre exemple avec des anneaux (noethériens en plus) on a l'inclusion de Z dans Q qui est un épimorphisme d'anneaux, évidemment pas surjectif.

[abcd22]

Pour montrer qu'un monomorphisme d’anneaux est injectif :
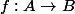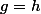Soit un monomorphisme d’anneaux. Soient tels que . On prend , le morphisme de dans qui envoie sur , le morphisme de dans qui envoie sur . On a bien , d’où et .

Rq : Pour montrer qu’un monomorphisme de modules est injectif on aurait pu utiliser la même technique en remplaçant C par et en envoyant 1 sur x et y.

[arsene]

Une de ces deux inclusions est très simple : laquelle ?

et
Bon aprem leon
J ai fait la demonstration de la 2eme inclusion simplement.La deuxieme me semble plus compliqué ke je ne lai fait.Car la notion maximal n est pas intervenu ds mon raisonnement.

[arsene]

Une de ces deux inclusions est très simple : laquelle ?

et
Bon aprem leon
J ai fait la demonstration de la 1ere inclusion simplement.La deuxieme me semble plus compliquée ke je ne lai faite.Car la notion maximal n est pas intervenue ds mon raisonnement.

Et l epi est defini sur un meme anneau R noetherien.
La question c est justement ceci un épimorphisme d'un anneau noetherien sur lui-même est-il injectif ?

[abcd22]

J ai fait la demonstration de la 2eme inclusion simplement.La deuxieme me semble plus compliqué ke je ne lai fait.Car la notion maximal n est pas intervenue ds mon raisonnement.

La maximalité doit forcément être utilisée car le résultat est faux avec des idéaux non maximaux, par exemple dans , avec A = 2;) et B = 4;), on a AB = 8;) et A inter B = B = 4;).

[arsene]

Et si on met des anneaux au lieu de modules ça ne marche plus car le noyau d'un morphisme d'anneaux n'est pas un anneau mais seulement un idéal, et ...

salut abcd22
tu vas loin avec les notions
je ne connais pas encore ce que c qu´un module
ma question etait
un épimorphisme d'un anneau noetherien sur lui-même est-il injectif ?
sinon je ve ke vs exhiber un contre exple svp

[arsene]

pour toi, c'est quoi un épimorphisme ?

c un morphisme simplifiable a droite.Les deux notions nont pas de rapport etepimorphisme et injection donc je dirais que la proposition est fausse mais trouver un contre exemple ...je ne parviens pas