Continuité de cosinus

[lucie68]

Bonjour,

je définis le cosinus géométriquement avec le cercle trigonométrique.
Et j'aurais besoin du fait que le cosinus est continu en 0.
Alors j'ai lu quelque part que , comme c'est une projection orthogonale alors il est continu..
Mais je ne vois pas du tout comment parler de continuité de projection orthogonale et pourquoi c'est vrai ..
Alors si vous pouviez m'éclairer, ce serait cool :)
Merci beaucoup !

[Ericovitchi]

Qualitativement :
En gros, une fonction est continue si quand sa variable varie infinitésimalement, ça entraîne aussi une variation infinitesimale de la fonction.
Géométriquement, ton cos est la projection d'un point du cercle de rayon 1 sur l'axe des x. Autour de zéro, la projection se confond avec le point d'abcisse 1 (et cos(0) = 1). Quand tu fais bouger infinitésimalement le point sur le cercle, la projection varie également infinitesimalement et continument. On ne voit pas bien comment elle pourait être discontinue en zéro.

Sinon tu peux le démontrer analytiquement en repartant de la définition de la continuité :

Tu te donne un et tu essayes de trouver un tel que
Un excellent exercice :zen:

Après il y a peut-être des considérations générales sur les projections (caractérisées par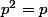 ) pour montrer qu'elles sont forcement continues à certaines condition mais là je laisse les éminents topologistes de ce forum le soin de dire ce qu'ils en pensent.

[ft73]

Bonjour,

je définis le cosinus géométriquement avec le cercle trigonométrique.
Et j'aurais besoin du fait que le cosinus est continu en 0.
Alors j'ai lu quelque part que , comme c'est une projection orthogonale alors il est continu..
Mais je ne vois pas du tout comment parler de continuité de projection orthogonale et pourquoi c'est vrai ..
Alors si vous pouviez m'éclairer, ce serait cool
Merci beaucoup !

A niveau élémentaire, je passerais par sin x <= x qui montre que sin est C^0 en 0, et donc cos aussi par la relation cos²+sin²=1.

[Skullkid]

En effet il me semble plus judicieux de passer par que tu peux démontrer en comparant les aires de triangles bien choisis sur la figure du cercle trigo.

En ce qui concerne l'histoire de la projection, c'est une application linéaire sur un espace de dimension finie, donc elle est continue. Cependant, en étant rigoureux, tu définis la fonction cos comme étant où f est la fonction qui à l'angle x associe le point correspondant sur le cercle trigo et i l'application qui au couple (x,y) associe le réel x. S'il est facile de démontrer que i est continue, je vois pas trop comment faire pour la continuité de f sans passer par la continuité de sin et de cos...

[lucie68]

Enfaite c'est justement pour démontrer que sin(x)<= x avec les aires que j'ai besoin de la continuité de cosinus.
Mais j'avais oublié el théorème qui dit qu'une application linéaire en dimension finie est continue, donc il me sauve :)
Merci !

[Ericovitchi]

sinon pour démontrer que sinx <=x avec des aires on peut aussi remarquer que l'aire du triangle marqué sur la figure est plus petite que l'aire du secteur.
l'aire du secteur vaut x/2
l'aire du triangle vaut sin (x) /2
donc sin (x) <= x