Détermination de complexe
17 messages
- Page 1 sur 1
Détermination de complexe
Bonjour !
Voila je révise pour demain je passe mon rattrapage de maths, je suis en licence d'info.
je n'arrive pas à résoudre cet exercice (qui été dans l'examen du premier semestre)
il faut déterminer tout les nombres complexe qui satisferont :
(z)^5 + 4(1-i) = 0
Voila si quelqu'un peut m'aider ( et je n'entend pas par "m'aider" me résoudre l'éxo, mais me donner une methode générale de résolution)
Merci d'avance ;)
Voila je révise pour demain je passe mon rattrapage de maths, je suis en licence d'info.
je n'arrive pas à résoudre cet exercice (qui été dans l'examen du premier semestre)
il faut déterminer tout les nombres complexe qui satisferont :
(z)^5 + 4(1-i) = 0
Voila si quelqu'un peut m'aider ( et je n'entend pas par "m'aider" me résoudre l'éxo, mais me donner une methode générale de résolution)
Merci d'avance ;)
baobab95 a écrit:non vraiment la je bloque désolé !
l'argument vaut - \Pi / 4.
je ne comprends pas d'où sors le 3i \Pi / 4.
et ici cela vaut dire qu'il faut élever le tout à la puissance 1/5 ?
Pense tu vraiment qu 'il y a une différence entre un argument de -pi/4 et un argument de 3pi/4.
Ce sont les deux les mêmes angles, à une question de convention près. Donc garde l'angle que tu préfère, c'est complètement pareil.
Maintenant applique la méthode que j'ai écrit 2 message plus haut.
En sachant que

on voit bien que l'on peut rajouter à l'exponentielle sans la modifier. C'est une période l'exponentielle complexe.
à l'exponentielle sans la modifier. C'est une période l'exponentielle complexe.
Cette technique te permet de pouvoir trouver les 5 racines que tu cherches. En effet, tu sais qu'il y en a 5 par le théorème fondamental de l'algèbre. Maintenant que ce passage est bon, tu fais

Comme on le voit clairment, c'est l'argument des nombres complexes que tu cherches. Par convention, ces argument doivent se trouver dans
c'est l'argument des nombres complexes que tu cherches. Par convention, ces argument doivent se trouver dans ) (ou
(ou ) , ce n'est qu'une question de convention). Sachant cela, tu va pouvoir trouver 5 nombre n entier tel que ton argument soit dans le bon domaine.
, ce n'est qu'une question de convention). Sachant cela, tu va pouvoir trouver 5 nombre n entier tel que ton argument soit dans le bon domaine.
Tu as donc trouvés tes 5 nombres complexes!
on voit bien que l'on peut rajouter
Cette technique te permet de pouvoir trouver les 5 racines que tu cherches. En effet, tu sais qu'il y en a 5 par le théorème fondamental de l'algèbre. Maintenant que ce passage est bon, tu fais
Comme on le voit clairment,
Tu as donc trouvés tes 5 nombres complexes!
desole, je n'ai pas eu le temps de me connecter hier soir.
Merci :we:
Oui, il y a bien une difference entre un argument de - et un argument de
et un argument de 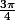 : l'argument doit etre choisi de telle sorte a ce que le module soit positif
: l'argument doit etre choisi de telle sorte a ce que le module soit positif
(ps super le tuto pour ecrire des belles formules mathématiques !!)
Merci :we:
switch_df a écrit:Pense tu vraiment qu 'il y a une différence entre un argument de -pi/4 et un argument de 3pi/4.
Oui, il y a bien une difference entre un argument de -
uztop a écrit: l'argument doit etre choisi de telle sorte a ce que le module soit positif
Qu'on m'arrête si je dis n'importe quoi, mais la détermination du domaine d'angle n'influence en rien le module d'un complexe. Un module négatif je vois pas comment, vu que c'est une norme qui par définition doit toujours être postive.
quel que soit r et quel que soit theta et quel que soit la détermination choisie pour les angles.
je disais ça en réponse à cette phrase:
Si tu ajoutes à l'argument, tu multiplies l'expression par -1. Or, comme le module doit nécessairement être positif, un argument de -pi/4 et un argument de 3pi/4 ce n'est pas la même chose.
à l'argument, tu multiplies l'expression par -1. Or, comme le module doit nécessairement être positif, un argument de -pi/4 et un argument de 3pi/4 ce n'est pas la même chose.
Je pense que tu voulais dire que -pi/4 et 7pi/4 c'est la même chose; là je suis d'accord.
Pense tu vraiment qu 'il y a une différence entre un argument de -pi/4 et un argument de 3pi/4.
Si tu ajoutes
Je pense que tu voulais dire que -pi/4 et 7pi/4 c'est la même chose; là je suis d'accord.
uztop a écrit:je disais ça en réponse à cette phrase:
Si tu ajoutesà l'argument, tu multiplies l'expression par -1. Or, comme le module doit nécessairement être positif, un argument de -pi/4 et un argument de 3pi/4 ce n'est pas la même chose.
Je pense que tu voulais dire que -pi/4 et 7pi/4 c'est la même chose; là je suis d'accord.
Ok, autant pour moi. Ca correspond pas. Je pensais à -pi/2 et 3pi/2... J'ai pas regardé les calculs, je pensais que ce qui l'embêtait c'était qu'une fois y'avait un signe moins et l'autre fois pas. C'est pour ça que j'ai insisté sur la détermination de l'angle.
Dsl
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
