Géometrie dans l'espace Ts

[Peutetre]

Bonjour !

J'ai un exercice de maths facultatif pour les vacances sur la géometrie dans l'éspace (chapitre dans le quel j'ai pas mal de difficulté...).

L'ensemble de l'éxercie repose sur la perpendicularité de 2 plans.

Donc un me donne : Soit ABCD un tétraédre régulier et soit I et J milieu réspectifs des séguement [AB] et [CD].

1/ Montrer que les plans (AJB) et (ICD) sont pérpendiculaires.

Je pense que pour demontrer ceci il suffit de montrer qu'un des 2 plans contient un droite hortogonal sécante a 2 droite de l'autre plan, mais je n'ai aucun idée de la procédure a employer pour cela...

Les autre questions sont assez proches de celle ci je cherche donc a avoir un exemple pour comprendre comment faire l'ensemble de l'éxos...

Merci d'avance !

[becirj]

Bonjour

Le triangle ACD est équilatéral puisque le tétraèdre est régulier, la médiane (AJ) est aussi hauteur donc
De même en utilisant le triagle (BCD),

Le plan (ICD) contient la droite (CD) orthogonale à 2 droites concourantes du plan (ABJ) donc les plans (ABJ) et (ICD) sont perpendiculaires.

[Peutetre]

Merci encor sa m'a permi de repondre au 2 question suivante c'est a dire :

-démontrer que (BCD) et (ACD) sont perpendiculair a (AJB)
-Et ques (AB) et (CD) sont perpendiculair.

Mais on me demande ensuite la nature de MNPQ sachant que M,N,P,Q milieux respéctif de AC, AD, BD, BC.

J'imagine qu'il sagit d'un rétangle mais je ne sais pas trop comment le démontre ??

[becirj]

Un peu de géométrie plane : dans le triangle ACD, M est le milieu de [AC] et N le mileiu de [AD] donc (théorème de Thalès ou homothétie de centre A de rapport )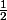
On démontre ainsi que chaque côté de MNPQ a pour longueur la moitié de la longueur de l'arête du tétraèdre, on a déjà un losange.
De plus, on démontrerait de la même manière que (MQ) est parallèle à (AB) et comme tu as démontré que les arêtes (AB) et (CD) sont orthogonales , on en déduit que ; MNPQ est donc un carré.

[Peutetre]

Merci encore pour les reponce précendente.

Il reste une derniere question du probleme au quel je n'arrive pas a repondre :

On me demande de montrer que : (IJ) est perpendiculaire au plan (MNPQ) en un point O. Dont il faut précisez la position dans le carré.

Merci d'avance.

Peut-etre.

[becirj]

(IJ) est perpendiculaire au plan (MNPQ) en un point O. Dont il faut précisez la position dans le carré.

Le triangle ABJ est isocèle (JA=JB), I étant le milieu de [AB], la médiane (JI) est aussi hauteur donc


On démontre de même dans CDI isocèle que et puisque (CD) est parallèle à (MN),

(IJ) est orthogonale à 2 droites sécantes du plan MNPQ donc (IJ) est orthogonale au plan (MNPQ)

Dans le triangle ABC, I milieu de [AB] et M milieu de [AC] donc
Dans le triangle DBC, J milieu de [DC] et P milieu de [DB] donc
On en déduit que ; IMJP est donc un parallélogramme, [IJ] et [MP] ont même milieu. Le milieu de [MP] est le centre du carré MNPQ donc le point d'intersection de (IJ) et du plan MNPQ est le centre du carré MNPQ.

On peut remarquer que l'on a en fait 3 carrés : MNPQ, IMJP, INJQ et ces 3 carrés ont le même centre.