Exercice équation différentielle

[Miko95]

Bonjour,

J'ai un exercice sur les équations différentielles que je n'arrive pas à résoudre à cause d'une valeur absolue qui me pose problème.

Sois l'équation différentielle dy/dt = 2*racine(abs(y)).
Je montre tout d'abord que la fonction y(t) = 0 est solution de l'équation.
Puis on me demande de trouver toutes les solutions de l'équation différentielle et la je bloque.Je sais que je dois traiter les deux cas: y(t)>0 et y(t)<0.

J'aurais besoin d'aide.
Merci d'avance

[JJa]

Bonjour,

Premièrement, le cas y>0 :
dy/dt = 2*racine(y)
dy/racine(y) = 2*dt que tu intègres.
Deuxièmement, le cas y<0 :
dy/dt = 2*racine(-y)
dy/racine(-y) = 2*dt que tu intègres.

[Miko95]

Merci pour la réponse mais j'ai déja fais cette étape(dsl je ne l'ai pas précisé).
Le problème est après l'integration ou je me retrouve avec une racine de y ou une racine de -y et je voudrais savoir est ce que ca pose des conditions pour la constante d'integration et pour t et si oui lesquels.

pour y>0:



Normalement,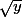 est positif donc l'est aussi, donc , est ce que c'est juste, est ce que la constante peut etre limité par rapport à t, c'est à ce niveau la que je comprend pas trop.
La meme incomprehension se pose pour le cas y<0.

Merci

[fourize]

bonjour,

Merci pour la réponse mais j'ai déja fais cette étape(dsl je ne l'ai pas précisé).
Le problème est après l'integration ou je me retrouve avec une racine de y ou une racine de -y et je voudrais savoir est ce que ca pose des conditions pour la constante d'integration et pour t et si oui lesquels.
Merci

déja en primitivant (integre comme vous dites); on fait + cte dans les deux membres. et puisqu'ici on cherche la fonction Y, tu seras obligé d'envoyer la cte de gauche à dte; ce qui donnera une autre cte qui, cette derniere sera la somme des deux precedentes.

par ailleurs en faisant la sommes de y et tu sera obliger aussi d'additionner les ctes pour en en avoir qu'une ...

bref: je te conseillerai de ne pas les mettres à chaque fois mais plus tot de la mettre une seule fois dans la solution generale :happy2:

pour y>0:

ta deuxieme parite

ATTENTION les constentes dependent pas des t et tu ne vas pas les
fixées positives...

[Miko95]

Oui c'est ce que j'ai fais, j'ai modifié le post... :)

[fourize]

re,

Oui c'est ce que j'ai fais, j'ai modifié le post...

essaie de faire le 1 cas en details dans ton prochain post... la j'ai pas trop bien compris car la solution generale devait etre Y + + cte.
avec la solution de l'équation sans second membre et Y la solution du premier ou du 2 cas .

[Miko95]

Merci pour la réponse donc ca se passe comment?
si C est inférieur à -t² alors C + t² est négatif est dans ce cas racine(y) devrait l'etre aussi selon l'égalité ce qui n'est pas possible donc je ne vois comment faire.

[Miko95]

Je fais le cas 1 :
si y > 0 alors:






Normalement j'arrive à là mais le truc c'est que je ne vois pas ce qu'il en est à propos de la constante C quand je suis à la ligne 2.

[fourize]

Je fais le cas 1 :
si y > 0 alors:

c'est ici ou je pensais t'aller faire des erreur avec ton C positive ... et les blabla que t'avais dit avant . mais c'est bon tu as eleveé au carré

.

et la tu developpe t'aura Y= et la: en faisant l'ddition de Y et ça donnera
f(t) = +
et tu posera k = C²+C' . comme ça dans la solution general tu n'as que K.

fin c'est une façon de parler mais il y aura le 2Ct (tu le supprime pas non plus )

[Miko95]

Merci pour la réponse mais je ne comprend pas pourquoi il ne devrait pas y avoir de condition pour le C avant d'élever au carré.A cette ligne, la ligne 2,

alors qu'à ce niveau il est clair que t + C doit etre positif et donc que si on choisit un C qui fait que t+C est négatif, il y a contradiction.
C'est ce problème avec lequel j'ai du mal.

Merci pour l'aide

[Miko95]

et la tu developpe t'aura Y=t^4 + 2Ct + C^2 et la: en faisant l'ddition de Y et y_0 ça donnera
f(t) = y_0 + c' +t^4 + 2Ct + C^2
et tu posera k = C²+C' . comme ça dans la solution general tu n'as que K.

fin c'est une façon de parler mais il y aura le 2Ct (tu le supprime pas non plus )

De plus j'ai pas vraiment compris ce que tu explique ici, au stade ou je suis normalement, j'ai la solution générale, pourquoi je rajoute ce y0 ou ce C' ?

[fourize]

Merci pour la réponse mais je ne comprend pas pourquoi il ne devrait pas y avoir de condition pour le C avant d'élever au carré.A cette ligne, la ligne 2,

alors qu'à ce niveau il est clair que t² + C doit etre positif et donc que si on choisit un C qui fait que t²+C est négatif, il y a contradiction.
C'est ce problème avec lequel j'ai du mal.
Merci pour l'aide

le terme t²+C est positif (je suis entierement d'accord) mais ce que me semble inacceptable est ton desire de vouloir limiter t ou C dans un domaine "positif" NON.
si la somme est positif et t est dans le domaine de définition (je suppose que tu le connais ) ça suffit largement.

ceci dit, si des conditions initiales pour calculer les constantes ... bah c'est parfait !

pourquoi je rajoute ce y0 ou ce C' ?

AH § la solution generale d'une équation differentille lineaire est la somme de la solutions particuliere(equation sans second membre ) et la solution avec seconds membres.

PS. j'espere que je t'apprends rien dans ce derniere paragraphes parce que si non c'est pas Superieur ! :doh:

[Miko95]

C'est bizarre, cette équation différentielle n'est pas linéaire il me semble?!
J'ai une racine de y, c'est pas de la forme d'une équation linéaire normalement?

[fourize]

re,

C'est bizarre, cette équation différentielle n'est pas linéaire il me semble?!
J'ai une racine de y, c'est pas de la forme d'une équation linéaire normalement?

OUPS ! je me suis un peu egaré avec un autre exercice que je suis entrain de traiter actuellement... (desolé pour la liéarité )

ceci etant, t'es bien d'accord que C est une constante. > ne doit pas etre limiter> et que seule t²+ C doit etre positif suffit?

pour rassembler les deux solutions. je trouve dans mes souvenirs les plus encienne "la methode de la variation de la cte". mais je me demande si elle est applicable dans ces genres d'équation :mur: